Todo sobre Vértices y Aristas de Cuerpos Geométricos: Guía Completa
Los cuerpos geométricos son figuras tridimensionales que encontramos en nuestra vida cotidiana, desde un cubo hasta una esfera. A menudo, al estudiar estas formas, nos encontramos con términos como «vértices» y «aristas». Pero, ¿qué significan realmente? ¿Por qué son importantes en la geometría? En esta guía completa, exploraremos en profundidad qué son los vértices y aristas de los cuerpos geométricos, cómo se relacionan entre sí y por qué su comprensión es fundamental para diversas aplicaciones en matemáticas, arquitectura y diseño. A lo largo de este artículo, descubrirás ejemplos prácticos, definiciones claras y datos interesantes que te ayudarán a apreciar la belleza de las formas tridimensionales. Así que, ¡prepárate para sumergirte en el fascinante mundo de los cuerpos geométricos!
¿Qué son los Vértices en Geometría?
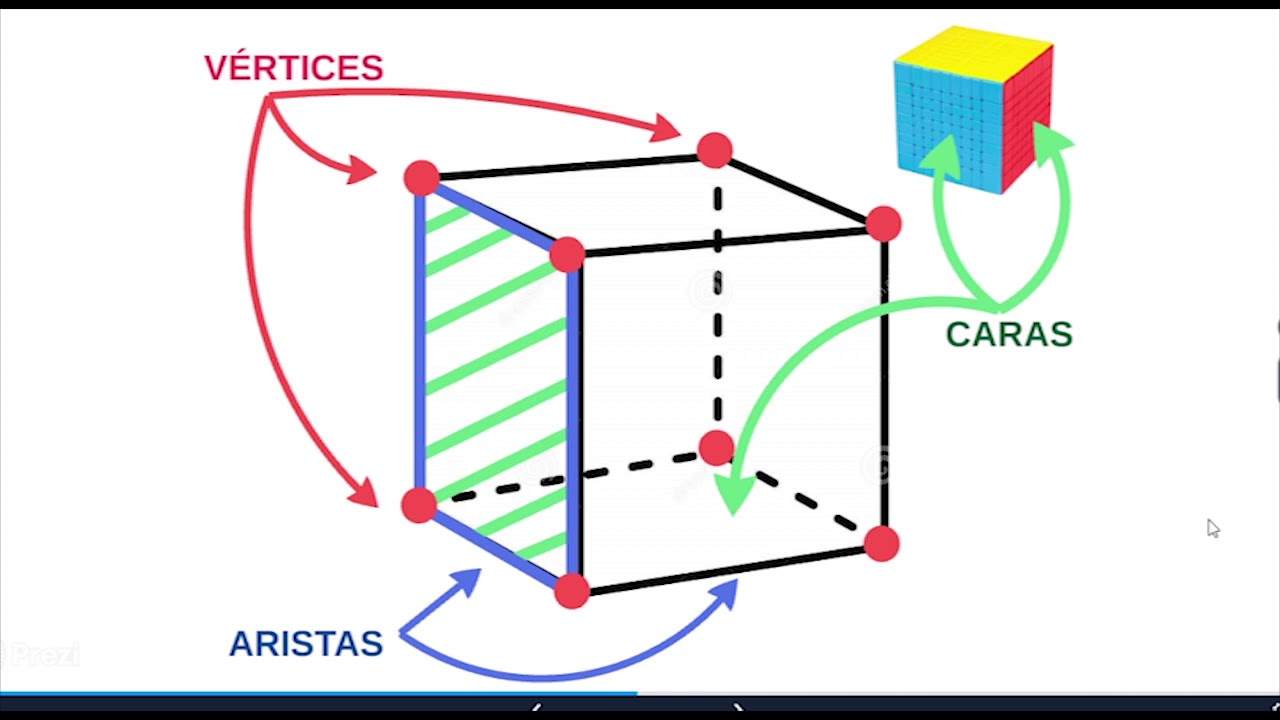
Los vértices son puntos clave en la estructura de los cuerpos geométricos. En términos simples, un vértice es un punto donde se encuentran dos o más aristas. En un cubo, por ejemplo, cada esquina es un vértice. Entender los vértices es esencial para visualizar y trabajar con diferentes formas tridimensionales.
Características de los Vértices
Los vértices tienen varias características interesantes que los distinguen:
- Conexión: Un vértice se forma donde se encuentran las aristas. En un cubo, hay 8 vértices, y cada uno está conectado a tres aristas.
- Dimensionalidad: Los vértices son fundamentales en la definición de la forma. Sin ellos, no podríamos describir un objeto tridimensional de manera efectiva.
- Variabilidad: Diferentes cuerpos geométricos tienen diferentes cantidades de vértices. Por ejemplo, un tetraedro tiene 4, mientras que un dodecaedro tiene 20.
Ejemplos de Vértices en Cuerpos Geométricos
Para entender mejor los vértices, consideremos algunos ejemplos:
- Cubo: 8 vértices.
- Prisma triangular: 6 vértices.
- Tetraedro: 4 vértices.
Estos ejemplos ilustran cómo la cantidad de vértices puede variar considerablemente entre diferentes cuerpos geométricos.
¿Qué son las Aristas en Geometría?
Las aristas son las líneas que conectan los vértices de un cuerpo geométrico. Son fundamentales para definir la estructura y forma de un objeto tridimensional. Sin aristas, no tendríamos la geometría que conocemos hoy. Cada arista representa una conexión entre dos puntos, y su comprensión es vital para el estudio de la geometría.
Características de las Aristas
Al igual que los vértices, las aristas tienen características que vale la pena destacar:
- Conectividad: Cada arista conecta dos vértices. Por ejemplo, en un cubo, cada arista conecta dos de sus ocho vértices.
- Longitud: La longitud de las aristas puede variar según el cuerpo geométrico. En un cubo, todas las aristas tienen la misma longitud, mientras que en un prisma, pueden ser diferentes.
- Tipología: Las aristas pueden ser clasificadas en aristas internas y externas, dependiendo de su posición en relación con el cuerpo.
Ejemplos de Aristas en Cuerpos Geométricos
Veamos algunos ejemplos de aristas en cuerpos geométricos:
- Cubo: 12 aristas.
- Tetraedro: 6 aristas.
- Octaedro: 12 aristas.
Estos ejemplos muestran cómo el número de aristas puede variar dependiendo de la forma del cuerpo geométrico.
Relación entre Vértices, Aristas y Caras
Una de las relaciones más interesantes en geometría es la que existe entre vértices, aristas y caras, conocida como la fórmula de Euler. Esta fórmula establece que, en un poliedro convexo, la relación se puede expresar como:
V – E + F = 2
donde V representa el número de vértices, E el número de aristas y F el número de caras. Esta relación es fundamental en el estudio de la geometría tridimensional y tiene aplicaciones en diversas áreas, como la arquitectura y el diseño gráfico.
Ejemplos de la Fórmula de Euler
Veamos cómo se aplica esta fórmula a algunos cuerpos geométricos:
- Cubo: 8 vértices, 12 aristas, 6 caras. Aplicando la fórmula: 8 – 12 + 6 = 2.
- Tetraedro: 4 vértices, 6 aristas, 4 caras. Aplicando la fórmula: 4 – 6 + 4 = 2.
Esta relación no solo es fascinante, sino que también proporciona una herramienta útil para verificar la estructura de diferentes cuerpos geométricos.
Aplicaciones Prácticas de Vértices y Aristas
La comprensión de los vértices y aristas va más allá de la teoría; tiene múltiples aplicaciones en la vida real. Desde la arquitectura hasta la animación por computadora, los conceptos de vértices y aristas son fundamentales para crear estructuras y modelos tridimensionales.
En la Arquitectura
Los arquitectos utilizan el conocimiento de vértices y aristas para diseñar edificios y otras estructuras. Cada punto de conexión en un diseño arquitectónico puede ser considerado un vértice, mientras que las líneas que conectan estos puntos son las aristas. Esto permite a los arquitectos crear diseños complejos y funcionales, asegurando que cada elemento esté correctamente alineado y estructurado.
En la Animación por Computadora
En la animación y el modelado 3D, los vértices y aristas son esenciales. Cada modelo tridimensional está compuesto por una malla de vértices y aristas que definen su forma. Los animadores manipulan estos puntos para dar vida a personajes y objetos, creando movimientos fluidos y realistas. Sin una comprensión adecuada de cómo funcionan estos elementos, sería difícil lograr resultados satisfactorios en la animación.
Vértices y Aristas en Matemáticas Avanzadas
En el ámbito de las matemáticas, el estudio de los vértices y aristas se extiende a conceptos más avanzados como la topología y la teoría de grafos. La teoría de grafos, en particular, estudia las relaciones entre vértices (nodos) y aristas (conexiones), y tiene aplicaciones en campos como la informática, la biología y la sociología.
Teoría de Grafos
La teoría de grafos es una rama de las matemáticas que se centra en el estudio de grafos, que son estructuras formadas por vértices y aristas. Estos grafos pueden ser utilizados para modelar redes de todo tipo, desde redes sociales hasta circuitos eléctricos. Cada vértice puede representar un elemento, mientras que las aristas representan las conexiones entre ellos.
Topología
La topología es otra área de las matemáticas donde los conceptos de vértices y aristas son fundamentales. Estudia las propiedades de los espacios que se mantienen invariantes bajo deformaciones continuas. En este contexto, los vértices y aristas pueden representar puntos y líneas en un espacio topológico, lo que permite explorar conceptos como la conectividad y la continuidad.
Preguntas Frecuentes (FAQ)
1. ¿Cuál es la diferencia entre un vértice y una arista?
Un vértice es un punto donde se encuentran dos o más aristas, mientras que una arista es una línea que conecta dos vértices. En otras palabras, los vértices son las esquinas de una figura, y las aristas son los bordes que las conectan. Esta distinción es crucial para entender la estructura de los cuerpos geométricos.
2. ¿Cómo se cuentan los vértices y aristas de un poliedro?
Para contar los vértices y aristas de un poliedro, simplemente debes identificar cada punto de conexión (vértice) y cada línea que conecta estos puntos (arista). Puedes hacerlo visualmente o utilizando un modelo físico. Es importante recordar que la fórmula de Euler puede ayudarte a verificar tus conteos.
3. ¿Por qué son importantes los vértices y aristas en la geometría?
Los vértices y aristas son fundamentales para definir la forma y estructura de los cuerpos geométricos. Sin ellos, no podríamos describir ni entender las figuras tridimensionales de manera efectiva. Además, su comprensión tiene aplicaciones prácticas en diversas áreas, como la arquitectura y la animación por computadora.
4. ¿Qué cuerpos geométricos tienen más vértices y aristas?
Los cuerpos geométricos que tienen más vértices y aristas son aquellos que son más complejos en su estructura. Por ejemplo, un dodecaedro tiene 20 vértices y 30 aristas, mientras que un icosaedro tiene 12 vértices y 30 aristas. Estos cuerpos son ejemplos de poliedros regulares, que tienen caras congruentes y ángulos equivalentes.
5. ¿Cómo se relacionan los vértices, aristas y caras en un poliedro?
La relación entre vértices, aristas y caras en un poliedro se puede expresar mediante la fórmula de Euler: V – E + F = 2. Aquí, V representa el número de vértices, E el número de aristas y F el número de caras. Esta relación es esencial para entender la geometría tridimensional y se aplica a todos los poliedros convexos.
6. ¿Existen cuerpos geométricos sin aristas?
Sí, existen cuerpos geométricos sin aristas, como la esfera. En una esfera, no hay aristas ni vértices, ya que su superficie es completamente suave y continua. Sin embargo, otros cuerpos geométricos, como los poliedros, siempre tendrán aristas y vértices debido a su estructura definida.
7. ¿Cómo se utilizan los vértices y aristas en la programación de gráficos por computadora?
En la programación de gráficos por computadora, los vértices y aristas se utilizan para crear modelos 3D. Cada modelo se representa como una malla de vértices y aristas, que se manipulan para formar figuras complejas. Los programadores utilizan estos conceptos para aplicar texturas, luces y animaciones, creando experiencias visuales envolventes.