Entendiendo el Valor Posicional de los Números Naturales: Guía Completa y Ejemplos

Los números son una parte fundamental de nuestras vidas, y entender su estructura es crucial para desarrollar habilidades matemáticas sólidas. Uno de los conceptos más importantes en matemáticas es el valor posicional, que se refiere a cómo el lugar que ocupa un dígito en un número determina su valor. En esta guía completa, exploraremos a fondo el valor posicional de los números naturales, desglosando sus componentes y ofreciendo ejemplos prácticos que facilitarán su comprensión. Aprenderás cómo funciona este sistema, su historia, su aplicación en la vida cotidiana y mucho más. Si alguna vez te has preguntado por qué el número 345 es diferente a 543, o cómo se construyen los números, este artículo es para ti.

¿Qué es el Valor Posicional?

El valor posicional es un sistema que asigna un valor específico a cada dígito de un número según su posición. En el sistema decimal, que es el más utilizado, cada posición representa una potencia de diez. Por ejemplo, en el número 345, el 3 representa 300, el 4 representa 40 y el 5 representa 5. Esta estructura permite que se formen números mucho más grandes de manera eficiente y comprensible.

La Base Decimal

El sistema decimal es un sistema de numeración en base 10, lo que significa que utiliza diez dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Cada uno de estos dígitos puede ocupar diferentes posiciones, y el valor de cada posición se multiplica por 10 elevado a la potencia correspondiente. Por ejemplo:

• En el número 2,345:
• 2 está en la posición de las miles (2 x 1,000)
• 3 está en la posición de las centenas (3 x 100)
• 4 está en la posición de las decenas (4 x 10)
• 5 está en la posición de las unidades (5 x 1)

Esto significa que el número 2,345 se puede descomponer como 2,000 + 300 + 40 + 5. Este descomposición es clave para entender el valor posicional.

Potencias de Diez

La comprensión de las potencias de diez es esencial para entender el valor posicional. Cada posición a la izquierda en un número representa un incremento de diez. Por ejemplo:

• 1 (10⁰)
• 10 (10¹)
• 100 (10²)
• 1,000 (10³)

Así, al leer un número, es importante reconocer qué potencia de diez representa cada dígito. Esta habilidad es fundamental en matemáticas, ya que permite realizar operaciones aritméticas y resolver problemas de manera más eficiente.

Ejemplos Prácticos de Valor Posicional

Para ilustrar mejor cómo funciona el valor posicional, veamos algunos ejemplos prácticos que desglosan diferentes números y sus significados. Este enfoque ayudará a clarificar cómo cada dígito contribuye al valor total del número.

Ejemplo 1: El Número 1,234

Analicemos el número 1,234:

• 1 está en la posición de los miles: 1 x 1,000 = 1,000
• 2 está en la posición de las centenas: 2 x 100 = 200
• 3 está en la posición de las decenas: 3 x 10 = 30
• 4 está en la posición de las unidades: 4 x 1 = 4

Por lo tanto, 1,234 se descompone en 1,000 + 200 + 30 + 4, lo que muestra cómo cada dígito contribuye a la suma total.

Ejemplo 2: El Número 56,789

Veamos otro ejemplo, el número 56,789:

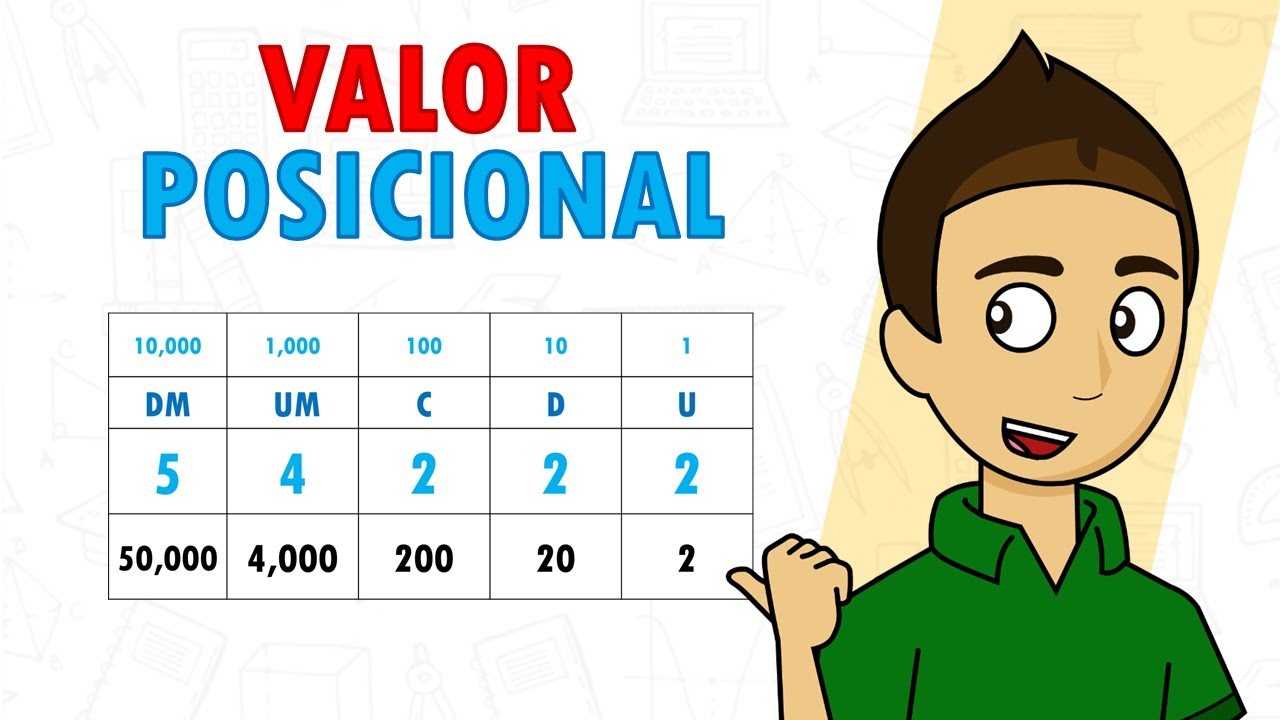
• 5 está en la posición de las decenas de mil: 5 x 10,000 = 50,000
• 6 está en la posición de las miles: 6 x 1,000 = 6,000
• 7 está en la posición de las centenas: 7 x 100 = 700
• 8 está en la posición de las decenas: 8 x 10 = 80
• 9 está en la posición de las unidades: 9 x 1 = 9

Así, 56,789 se descompone en 50,000 + 6,000 + 700 + 80 + 9. Este ejemplo demuestra cómo el valor posicional permite que números grandes sean manejables y comprensibles.

La Historia del Sistema de Numeración Posicional

El sistema de numeración posicional tiene una rica historia que se remonta a civilizaciones antiguas. Su desarrollo ha sido crucial para la evolución de las matemáticas y la contabilidad. En esta sección, exploraremos sus orígenes y cómo ha llegado a ser el sistema que conocemos hoy.

Orígenes Antiguos

Las primeras civilizaciones, como los babilonios y los egipcios, usaban sistemas de numeración que no eran posicionales. Por ejemplo, los babilonios utilizaban un sistema sexagesimal (base 60) que limitaba su capacidad para expresar grandes números de manera eficiente. Por otro lado, los egipcios usaban jeroglíficos para representar cantidades, pero cada símbolo tenía un valor fijo, lo que hacía que los cálculos fueran complicados.

La Influencia India y Árabe

El verdadero avance hacia el sistema posicional que conocemos hoy proviene de la India, donde se desarrolló el concepto del cero y la notación decimal. Este sistema fue luego adoptado por los matemáticos árabes, quienes lo llevaron a Europa durante la Edad Media. La introducción del cero fue un cambio revolucionario, ya que permitió a los matemáticos expresar números de forma más compacta y realizar cálculos más complejos.

La Adopción en Europa

A medida que el sistema posicional se difundió en Europa, se hizo evidente su eficacia en comparación con los sistemas anteriores, como el ábaco o la numeración romana. Durante el Renacimiento, el uso de la notación decimal se consolidó, y hoy es el sistema estándar en todo el mundo. Esta evolución ha permitido que las matemáticas avancen, facilitando el comercio, la ciencia y la tecnología.

Aplicaciones del Valor Posicional en la Vida Cotidiana

El valor posicional no es solo un concepto teórico; tiene aplicaciones prácticas en nuestra vida diaria. Desde la gestión de finanzas personales hasta el uso de tecnología, entender cómo funciona puede mejorar nuestra toma de decisiones. Veamos algunas aplicaciones clave.

Finanzas Personales

Cuando manejamos nuestro dinero, el valor posicional se vuelve evidente en cómo interpretamos cifras en extractos bancarios o facturas. Por ejemplo, si ves un saldo de $1,250, puedes descomponerlo en 1,000 + 200 + 50 + 0. Esta habilidad no solo te ayuda a entender tus finanzas, sino que también te permite realizar cálculos mentales rápidos para presupuestos y ahorros.

Uso de Tecnología

La programación y el desarrollo de software también dependen del valor posicional. Los números binarios, que utilizan solo dos dígitos (0 y 1), son la base de toda la tecnología digital. Aquí, cada posición representa una potencia de dos. Comprender el valor posicional en diferentes bases, como binario o hexadecimal, es crucial para quienes trabajan en campos de la computación.

Educación Matemática

En el ámbito educativo, enseñar el valor posicional es fundamental para que los estudiantes desarrollen habilidades matemáticas sólidas. Al comprender cómo se construyen los números, los estudiantes pueden abordar operaciones matemáticas más complejas, como la suma y la resta, de manera más efectiva. Además, esta comprensión les proporciona una base sólida para temas avanzados en matemáticas y ciencias.

Preguntas Frecuentes (FAQ)

1. ¿Por qué es importante entender el valor posicional?

Entender el valor posicional es fundamental para realizar operaciones matemáticas, interpretar cifras y desarrollar habilidades numéricas. Este conocimiento es esencial no solo en matemáticas, sino también en situaciones cotidianas como la gestión de finanzas personales.

2. ¿Cómo se enseña el valor posicional a los niños?

La enseñanza del valor posicional a los niños se puede hacer a través de juegos, actividades prácticas y visualizaciones. Usar bloques o tarjetas con números puede ayudar a los niños a ver cómo los dígitos cambian de valor según su posición, facilitando así su comprensión.

3. ¿Qué diferencias hay entre el sistema decimal y otros sistemas de numeración?

El sistema decimal es un sistema posicional en base 10, mientras que otros sistemas, como el binario (base 2) o el hexadecimal (base 16), utilizan diferentes bases. Cada sistema tiene su propio conjunto de reglas y aplicaciones, y comprender estas diferencias es importante para trabajar en matemáticas y computación.

4. ¿Cómo se relaciona el valor posicional con el concepto de cero?

El cero es fundamental en el valor posicional porque permite que se representen números en un sistema posicional de manera compacta. Sin el cero, sería difícil distinguir entre números como 10 y 1,000. Su inclusión en el sistema decimal revolucionó las matemáticas y la contabilidad.

5. ¿Puedo aplicar el valor posicional en otros sistemas de numeración?

Sí, el concepto de valor posicional se aplica en cualquier sistema de numeración posicional, como el binario o el hexadecimal. Cada posición en estos sistemas representa una potencia de su base correspondiente, lo que permite realizar cálculos y operaciones de manera similar a como lo hacemos en el sistema decimal.

6. ¿Cuáles son algunos errores comunes al aprender sobre el valor posicional?

Algunos errores comunes incluyen confundir el valor de un dígito con su posición, no entender la importancia del cero o tener dificultades para descomponer números en sus valores posicionales. Practicar con ejemplos y actividades puede ayudar a superar estos desafíos.

7. ¿El valor posicional se utiliza en otras disciplinas además de las matemáticas?

Sí, el valor posicional se utiliza en diversas disciplinas, como la informática, la contabilidad y la ingeniería. En programación, por ejemplo, comprender cómo se representan los datos en diferentes bases es crucial para el desarrollo de software y el análisis de datos.