¿Qué es el Numerador en una Fracción? Definición y Ejemplos Claros

Cuando hablamos de fracciones, es común encontrar términos que pueden parecer confusos a primera vista. Uno de esos términos es el «numerador». Comprender qué es el numerador en una fracción es esencial para dominar conceptos matemáticos básicos y avanzados. Este artículo no solo te proporcionará una definición clara, sino que también explorará su función, su relación con el denominador y ofrecerá ejemplos prácticos para ilustrar su uso. A lo largo de este recorrido, descubrirás cómo el numerador juega un papel fundamental en el ámbito de las matemáticas, permitiéndote realizar cálculos con mayor facilidad y precisión. Si alguna vez te has preguntado sobre la importancia del numerador y cómo se utiliza en diferentes contextos, ¡sigue leyendo!

Definición de Numerador

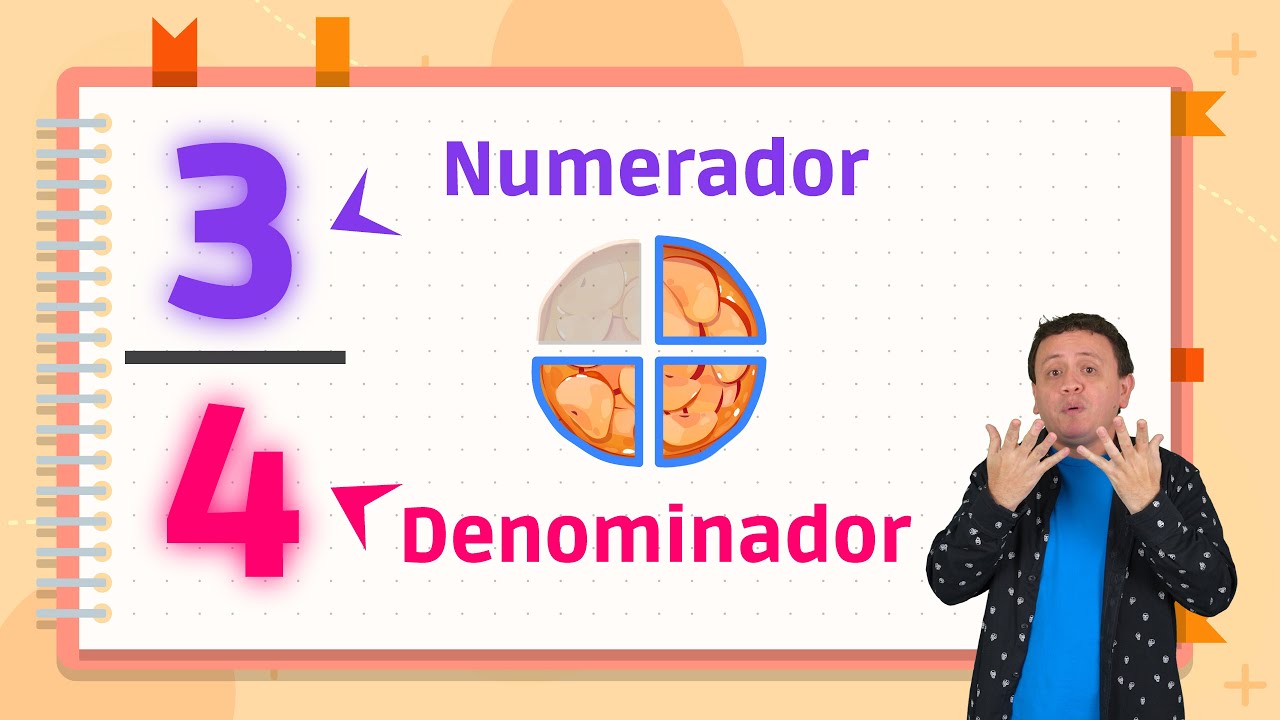
El numerador es el número que se encuentra en la parte superior de una fracción. Representa la cantidad de partes que se consideran o se toman de un todo. Por ejemplo, en la fracción 3/4, el número 3 es el numerador. Esto significa que estamos tomando 3 partes de un total de 4 partes iguales. Es fundamental entender que el numerador no solo indica una cantidad, sino que también establece una relación con el denominador, que es el número que se encuentra en la parte inferior de la fracción y que indica cuántas partes iguales hay en total.

El numerador puede ser cualquier número entero, positivo o negativo, así como también puede ser un número decimal o fraccionario en situaciones más avanzadas. Sin embargo, en el contexto más básico de las fracciones, normalmente se trabaja con números enteros. El concepto de numerador es crucial en diversas aplicaciones matemáticas, desde la aritmética básica hasta el cálculo y más allá.

Ejemplos de Numeradores en Fracciones

Para ilustrar mejor el concepto de numerador, consideremos algunos ejemplos:

• En la fracción 1/2, el numerador es 1. Esto significa que estamos tomando 1 parte de un total de 2 partes iguales.
• En la fracción 5/8, el numerador es 5, lo que indica que estamos considerando 5 partes de un total de 8 partes.
• En la fracción 7/10, el numerador es 7, indicando que tomamos 7 partes de un total de 10.

Estos ejemplos demuestran cómo el numerador define la porción de un total que se está considerando. Cuanto mayor sea el numerador en relación con el denominador, mayor será la fracción resultante.

La Relación entre Numerador y Denominador

Entender la relación entre el numerador y el denominador es clave para comprender cómo funcionan las fracciones. El denominador, que se encuentra en la parte inferior, indica cuántas partes iguales conforman el todo. Por lo tanto, el numerador y el denominador trabajan juntos para representar una fracción. Esta relación se puede expresar como una razón o proporción. Por ejemplo, en la fracción 3/4, el numerador 3 indica que estamos tomando 3 partes, mientras que el denominador 4 indica que hay un total de 4 partes.

Es importante destacar que si el numerador es igual al denominador, la fracción es igual a 1. Por ejemplo, en 4/4, tanto el numerador como el denominador son 4, lo que representa el total completo. Por otro lado, si el numerador es mayor que el denominador, como en 5/4, se obtiene una fracción impropia, que también se puede convertir a un número mixto, en este caso, 1 1/4.

Ejemplos de Fracciones con Diferentes Numeradores

Para comprender mejor esta relación, veamos algunos ejemplos:

• En la fracción 2/3, el numerador 2 indica que estamos considerando 2 partes de un total de 3.
• Si cambiamos a 3/3, el numerador es igual al denominador, lo que significa que estamos considerando el total, es decir, 1.
• En 5/3, el numerador es mayor que el denominador, lo que representa una fracción impropia que puede ser expresada como 1 2/3.

Estos ejemplos ilustran cómo el numerador afecta la interpretación de la fracción en relación con el denominador.

Cómo Calcular el Valor de una Fracción a partir del Numerador

El valor de una fracción se puede calcular dividiendo el numerador por el denominador. Esta operación es fundamental para entender cómo funcionan las fracciones y para realizar cálculos matemáticos más complejos. Por ejemplo, en la fracción 3/4, el valor se calcula como 3 dividido por 4, lo que resulta en 0.75. Este proceso es aplicable a cualquier fracción, y comprenderlo es esencial para el manejo de fracciones en diversas situaciones matemáticas.

Ejemplo Práctico de Cálculo de Fracciones

Consideremos el cálculo del valor de varias fracciones:

• Para la fracción 2/5: 2 dividido por 5 es igual a 0.4.
• Para la fracción 7/8: 7 dividido por 8 es igual a 0.875.
• Para la fracción 1/3: 1 dividido por 3 es aproximadamente 0.333.

Estos cálculos son útiles en una variedad de contextos, como en la cocina, la construcción y la estadística, donde a menudo se necesita convertir fracciones a decimales para facilitar la interpretación de los datos.

Aplicaciones del Numerador en la Vida Cotidiana

El concepto de numerador y fracciones, en general, tiene múltiples aplicaciones en nuestra vida diaria. Desde situaciones cotidianas hasta campos más técnicos, las fracciones son herramientas matemáticas que utilizamos sin darnos cuenta. Por ejemplo, al cocinar, las recetas a menudo requieren fracciones de ingredientes. Si una receta pide 2/3

Otras Aplicaciones Comunes

Además de la cocina, aquí hay algunas aplicaciones adicionales del numerador en la vida cotidiana:

• Finanzas: Al calcular porcentajes de descuentos o intereses, a menudo se utilizan fracciones donde el numerador representa la cantidad de dinero que se ahorra o se gana.
• Construcción: En proyectos de construcción, se utilizan fracciones para medir longitudes y materiales. Por ejemplo, si necesitas 3/8 de una tabla, el numerador indica cuántas partes de una tabla completa se requieren.
• Educación: En el aula, los maestros utilizan fracciones para enseñar conceptos de división y proporción, ayudando a los estudiantes a comprender la relación entre diferentes cantidades.

Estas aplicaciones demuestran cómo el numerador y las fracciones son componentes fundamentales de la matemática que influyen en diversas áreas de nuestras vidas.

Errores Comunes Relacionados con el Numerador

Aunque el concepto de numerador puede parecer simple, hay algunos errores comunes que las personas suelen cometer al trabajar con fracciones. Uno de los más frecuentes es confundir el numerador con el denominador. Es importante recordar que el numerador representa las partes que se toman, mientras que el denominador indica el total de partes. Este error puede llevar a confusiones en cálculos y resultados incorrectos.

Ejemplos de Errores Comunes

Veamos algunos ejemplos de errores comunes:

• Al sumar fracciones, algunas personas pueden sumar los numeradores y denominadores incorrectamente. Por ejemplo, al sumar 1/4 + 1/4, el resultado correcto es 2/4, no 1/8.
• Otro error común es no simplificar fracciones. Por ejemplo, en lugar de reconocer que 4/8 se puede simplificar a 1/2, algunas personas pueden dejar la fracción en su forma original, lo que puede dificultar la comprensión.

Ser consciente de estos errores puede ayudarte a mejorar tus habilidades matemáticas y a trabajar con fracciones de manera más efectiva.

Preguntas Frecuentes (FAQ)

1. ¿Qué representa el numerador en una fracción?

El numerador en una fracción representa la cantidad de partes que se están considerando de un total. Es el número que se encuentra en la parte superior de la fracción y se utiliza en conjunto con el denominador para indicar una porción de un todo.

2. ¿Puede el numerador ser un número decimal?

Sí, el numerador puede ser un número decimal en fracciones más complejas. Sin embargo, en la mayoría de los casos básicos, se trabaja con números enteros. Por ejemplo, en la fracción 1.5/3, el numerador es 1.5.

3. ¿Cómo se simplifica una fracción con un numerador mayor que el denominador?

Cuando el numerador es mayor que el denominador, se puede simplificar la fracción convirtiéndola en un número mixto. Por ejemplo, la fracción 9/4 se puede simplificar a 2 1/4, donde 2 es el número entero y 1/4 es la parte fraccionaria.

4. ¿Cuál es la importancia del numerador en la resolución de problemas matemáticos?

El numerador es fundamental en la resolución de problemas matemáticos porque determina la cantidad que se está considerando de un total. Sin una comprensión clara del numerador, es difícil realizar operaciones precisas con fracciones y resolver problemas en contextos matemáticos y de la vida cotidiana.

5. ¿Cómo se relaciona el numerador con el concepto de porcentaje?

El numerador se relaciona con el concepto de porcentaje porque los porcentajes son fracciones que se expresan sobre un total de 100. Por ejemplo, si tienes un numerador de 25 sobre un denominador de 100, esto representa el 25%. Comprender el numerador es esencial para calcular y entender porcentajes.

6. ¿Qué sucede si el numerador es cero?

Si el numerador es cero, la fracción es igual a cero, independientemente del valor del denominador, siempre que este no sea cero. Por ejemplo, en la fracción 0/5, el resultado es 0. Sin embargo, una fracción con un numerador de cero y un denominador de cero, como 0/0, es indefinida.

7. ¿El numerador siempre debe ser menor que el denominador?

No, el numerador no siempre debe ser menor que el denominador. Cuando el numerador es mayor que el denominador, se habla de fracciones impropias. Estas fracciones pueden ser convertidas en números mixtos, pero ambas formas son válidas y se utilizan en matemáticas.