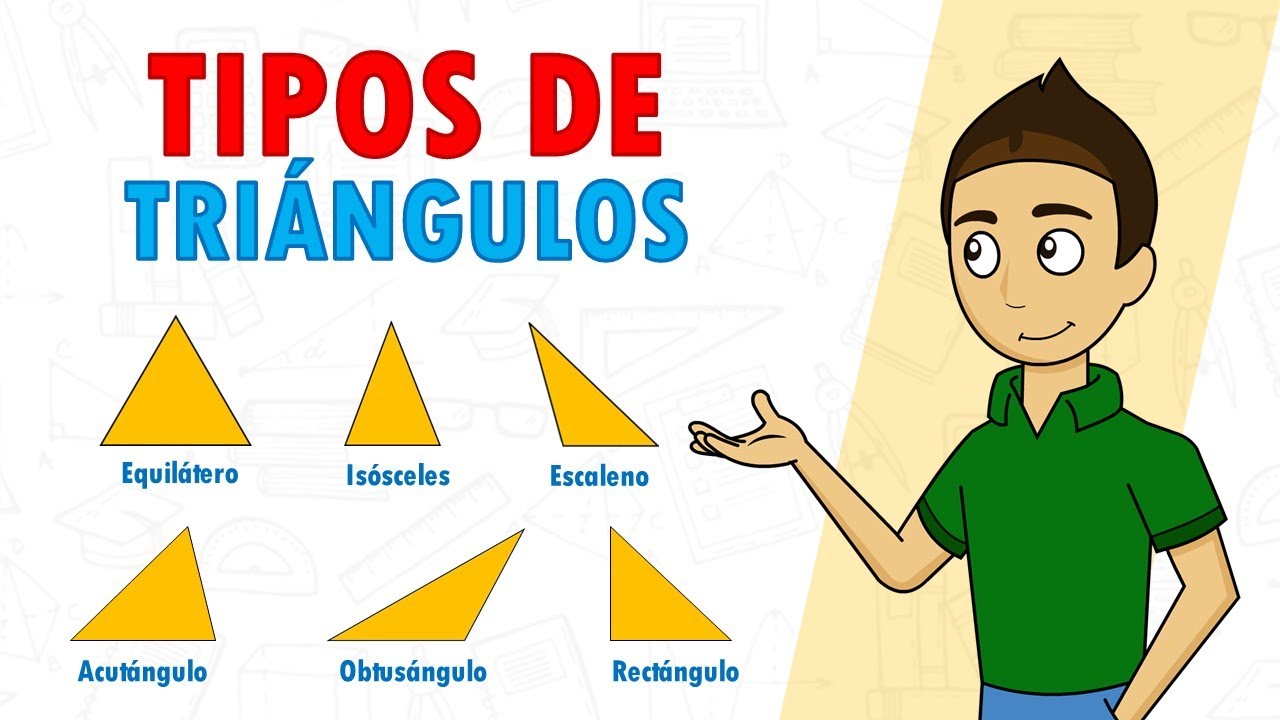
Guía Completa: Nombres de los Triángulos Según sus Lados
Los triángulos son figuras geométricas fundamentales que no solo se encuentran en el ámbito de la matemática, sino que también juegan un papel importante en la arquitectura, el arte y la naturaleza. Comprender los diferentes tipos de triángulos según sus lados es esencial para cualquier estudiante de matemáticas, arquitecto o entusiasta de la geometría. En esta guía completa, exploraremos los nombres y características de los triángulos, desde los más comunes hasta los menos conocidos, además de ofrecer ejemplos y aplicaciones prácticas. Si alguna vez te has preguntado cómo clasificar un triángulo o qué lo hace único, este artículo es para ti. Prepárate para sumergirte en el fascinante mundo de los triángulos y descubrir todo lo que necesitas saber sobre sus nombres según sus lados.
Clasificación de los Triángulos según sus Lados
Los triángulos se pueden clasificar de varias maneras, pero una de las más comunes es según la longitud de sus lados. Esta clasificación es fundamental porque determina no solo el nombre del triángulo, sino también sus propiedades y características geométricas. Existen tres tipos principales de triángulos según sus lados: equiláteros, isósceles y escalenos.
Triángulos Equiláteros
Un triángulo equilátero es aquel que tiene los tres lados de igual longitud. Además de la igualdad en sus lados, los triángulos equiláteros presentan algunas propiedades interesantes. Por ejemplo, cada uno de sus ángulos internos mide 60 grados, lo que los convierte en triángulos regulares. Esta simetría no solo es visualmente atractiva, sino que también tiene aplicaciones en diversas áreas, como la ingeniería y la arquitectura.
En términos de cálculo, el área de un triángulo equilátero se puede calcular usando la fórmula:
Área = (L^2 * √3) / 4
donde L es la longitud de un lado. Imagina que tienes un triángulo equilátero con lados de 4 cm. Aplicando la fórmula, obtendrás un área de aproximadamente 6.93 cm². Esta propiedad es útil en situaciones donde se necesita calcular espacios o materiales en proyectos de construcción.
Triángulos Isósceles
Los triángulos isósceles son aquellos que tienen al menos dos lados de igual longitud. Esta característica no solo les otorga un nombre, sino que también implica que los ángulos opuestos a los lados iguales son congruentes. Por ejemplo, si un triángulo tiene lados de 5 cm, 5 cm y 3 cm, los ángulos opuestos a los lados de 5 cm serán iguales. Esta propiedad se utiliza frecuentemente en problemas de geometría, donde se necesita determinar ángulos o lados desconocidos.
El área de un triángulo isósceles se puede calcular de varias maneras, pero una de las más comunes es usando la altura. Si conoces la base (el lado desigual) y la altura desde el vértice opuesto, puedes usar la fórmula:
Área = (Base * Altura) / 2
Por ejemplo, si la base mide 6 cm y la altura desde el vértice opuesto mide 4 cm, el área será de 12 cm². Esto muestra cómo los triángulos isósceles son prácticos en aplicaciones reales, como la construcción de techos o estructuras que requieren simetría.
Triángulos Escalenos
Los triángulos escalenos son aquellos que tienen los tres lados de diferentes longitudes. Esta variedad ofrece una gran diversidad en términos de forma y ángulos. En un triángulo escaleno, los ángulos internos también son diferentes entre sí, lo que significa que no hay simetría en esta figura. Un ejemplo común de un triángulo escaleno sería uno con lados de 3 cm, 4 cm y 5 cm.
La falta de simetría en los triángulos escalenos puede hacer que su análisis sea un poco más complejo. Sin embargo, se pueden aplicar diversas fórmulas para calcular su área, como la fórmula de Herón, que es especialmente útil cuando se conocen los tres lados:
s = (a + b + c) / 2
Área = √(s * (s – a) * (s – b) * (s – c))
donde a, b y c son las longitudes de los lados. Usando el ejemplo anterior, el área del triángulo escaleno sería aproximadamente 6 cm². Esta fórmula es invaluable en situaciones donde se necesita calcular áreas sin tener que conocer la altura.
Propiedades Geométricas de los Triángulos
Además de su clasificación, los triángulos tienen propiedades geométricas únicas que los hacen fascinantes. Comprender estas propiedades es esencial para resolver problemas de geometría y aplicar conceptos en situaciones del mundo real.
La Suma de los Ángulos Internos
Una de las propiedades más básicas pero fundamentales de los triángulos es que la suma de sus ángulos internos siempre es igual a 180 grados. Esto se aplica a todos los tipos de triángulos, ya sean equiláteros, isósceles o escalenos. Por ejemplo, en un triángulo equilátero, cada ángulo mide 60 grados, mientras que en un triángulo escaleno, los ángulos pueden variar, pero su suma seguirá siendo 180 grados.
Este concepto es crucial en la resolución de problemas, ya que permite deducir el valor de un ángulo si se conocen los otros dos. Imagina que tienes un triángulo con ángulos de 70 y 50 grados; puedes calcular el tercer ángulo restando la suma de los conocidos de 180, lo que da 60 grados. Esta propiedad es una herramienta esencial en la geometría y se aplica en múltiples contextos.
Desigualdad Triangular
Otra propiedad importante es la desigualdad triangular, que establece que la suma de las longitudes de dos lados de un triángulo siempre debe ser mayor que la longitud del tercer lado. Esto se puede expresar matemáticamente como: a + b > c, a + c > b, y b + c > a, donde a, b y c son las longitudes de los lados. Esta propiedad es fundamental para determinar si tres segmentos pueden formar un triángulo.
Por ejemplo, si tienes lados de 3 cm, 4 cm y 8 cm, no se puede formar un triángulo, ya que la suma de 3 y 4 no es mayor que 8. Este principio se utiliza en la construcción y diseño, asegurando que las estructuras sean viables y estables.
Ejemplos Prácticos de Triángulos en la Vida Cotidiana
Los triángulos no son solo un concepto abstracto; están presentes en nuestra vida diaria de muchas maneras. Desde la arquitectura hasta el diseño gráfico, su aplicación es amplia y variada. Aquí exploramos algunos ejemplos prácticos que ilustran la importancia de los triángulos en diferentes contextos.
Arquitectura y Construcción
En el campo de la arquitectura, los triángulos son esenciales para crear estructuras estables y estéticamente agradables. Los triángulos se utilizan en techos, puentes y otras construcciones para distribuir cargas y proporcionar soporte. Por ejemplo, los arcos de un puente suelen estar diseñados en forma triangular, lo que les permite soportar grandes pesos y resistir fuerzas externas, como el viento.
La utilización de triángulos en la arquitectura también se ve en el diseño de techos a dos aguas, donde los triángulos forman la base de la estructura, asegurando que el agua de lluvia drene correctamente y evitando la acumulación de peso que podría dañar el edificio.
Diseño Gráfico y Arte
En el diseño gráfico, los triángulos se utilizan para crear composiciones visuales dinámicas. Su forma puede atraer la atención del espectador y dirigir la mirada hacia puntos focales dentro de una imagen o diseño. Los triángulos también se emplean en logotipos y marcas para transmitir estabilidad y fuerza, ya que su forma angular sugiere movimiento y dirección.
Artistas de diversas disciplinas han incorporado triángulos en sus obras, utilizando la simetría y las proporciones para crear un impacto visual. Desde las obras de arte abstracto hasta las ilustraciones modernas, los triángulos son una herramienta valiosa en la expresión artística.
Triángulos en Matemáticas y Física
Los triángulos también tienen un papel fundamental en las matemáticas y la física. En matemáticas, se utilizan para resolver problemas relacionados con la geometría, trigonometría y álgebra. Por ejemplo, el teorema de Pitágoras, que se aplica a triángulos rectángulos, establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Esta relación es clave para calcular distancias y resolver problemas en diversas disciplinas.
Trigonometría y Triángulos
La trigonometría se basa en las relaciones entre los ángulos y los lados de los triángulos. Los triángulos rectángulos son especialmente importantes en esta área, ya que permiten definir funciones trigonométricas como el seno, coseno y tangente. Estas funciones se utilizan en diversas aplicaciones, desde la navegación hasta la ingeniería y la física.
Por ejemplo, al calcular la altura de un objeto utilizando un triángulo rectángulo, se puede aplicar la función tangente para determinar la relación entre la altura y la distancia desde el observador. Esta aplicación es fundamental en campos como la topografía y la astronomía.
Física y Triángulos
En física, los triángulos se utilizan para representar fuerzas y vectores. El método del triángulo de fuerzas es una técnica que permite sumar fuerzas que actúan en un objeto, utilizando triángulos para visualizar la dirección y magnitud de cada fuerza. Este enfoque es crucial en el estudio de la mecánica y la dinámica, ayudando a resolver problemas complejos de movimiento y equilibrio.
FAQ (Preguntas Frecuentes)
1. ¿Cuáles son las características de un triángulo equilátero?
Un triángulo equilátero tiene los tres lados de igual longitud y, por lo tanto, los tres ángulos internos miden 60 grados cada uno. Esta simetría lo convierte en un triángulo regular, y sus propiedades son útiles en diversas aplicaciones, desde la geometría hasta la arquitectura.
2. ¿Qué define a un triángulo isósceles?
Un triángulo isósceles tiene al menos dos lados de igual longitud. Los ángulos opuestos a estos lados también son iguales. Esta propiedad es útil en problemas de geometría y se aplica en situaciones donde se necesita determinar longitudes o ángulos desconocidos.
3. ¿Cómo se calcula el área de un triángulo escaleno?
El área de un triángulo escaleno se puede calcular utilizando la fórmula de Herón. Primero, se calcula el semiperímetro y luego se aplica la fórmula: Área = √(s * (s – a) * (s – b) * (s – c)), donde a, b y c son las longitudes de los lados del triángulo.
4. ¿Qué es la desigualdad triangular?
La desigualdad triangular establece que la suma de las longitudes de dos lados de un triángulo siempre debe ser mayor que la longitud del tercer lado. Esta propiedad es esencial para determinar si tres segmentos pueden formar un triángulo y se aplica en diversas áreas, incluyendo la construcción y diseño.
5. ¿Cómo se relacionan los triángulos con la trigonometría?
Los triángulos son fundamentales en trigonometría, especialmente los triángulos rectángulos, que permiten definir funciones trigonométricas como seno, coseno y tangente. Estas funciones son esenciales para resolver problemas de ángulos y distancias en matemáticas y física.
6. ¿Por qué son importantes los triángulos en la arquitectura?
Los triángulos son esenciales en arquitectura porque proporcionan estabilidad y soporte a las estructuras. Se utilizan en techos, puentes y arcos para distribuir cargas y resistir fuerzas externas. Su forma geométrica permite crear construcciones duraderas y estéticamente agradables.
7. ¿Existen otros tipos de triángulos además de los mencionados?
Además de los triángulos equiláteros, isósceles y escalenos, también existen triángulos rectángulos, que tienen un ángulo de 90 grados, y triángulos obtusángulos, que tienen un ángulo mayor a 90 grados. Cada tipo de triángulo tiene propiedades únicas y aplicaciones en diversas áreas.