# Guía Completa de Formulario de Áreas, Perímetros y Volúmenes: Todo lo que Necesitas Saber
La geometría es una parte fundamental de las matemáticas que nos rodea en la vida cotidiana. Desde calcular el espacio que ocupa un mueble en nuestra casa hasta entender la superficie de una piscina, las áreas, los perímetros y los volúmenes son conceptos que nos ayudan a resolver problemas prácticos. Esta Guía Completa de Formulario de Áreas, Perímetros y Volúmenes: Todo lo que Necesitas Saber está diseñada para ofrecerte un recurso integral donde descubrirás las fórmulas esenciales, sus aplicaciones y ejemplos que te ayudarán a dominar estos conceptos.
En este artículo, exploraremos cada uno de estos aspectos en detalle. Comenzaremos con una introducción a los conceptos básicos, luego pasaremos a las fórmulas específicas para diferentes figuras geométricas, y finalmente, responderemos algunas preguntas frecuentes para asegurar que tengas toda la información que necesitas. ¡Vamos a sumergirnos en el fascinante mundo de las áreas, perímetros y volúmenes!
## 1. Fundamentos de Áreas, Perímetros y Volúmenes
### 1.1 ¿Qué son el área, el perímetro y el volumen?
Para entender bien las fórmulas y su aplicación, es esencial conocer qué son el área, el perímetro y el volumen.
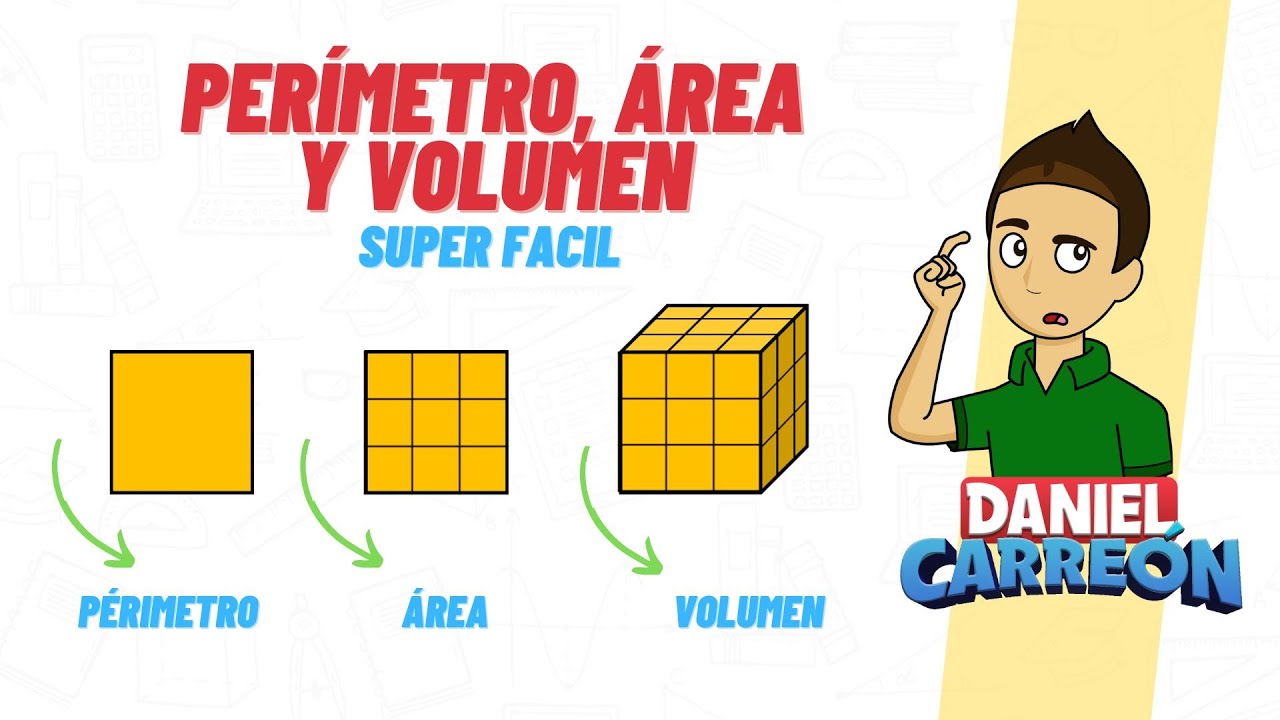
– Área: Es la medida de la superficie de una figura. Se expresa en unidades cuadradas, como metros cuadrados (m²) o centímetros cuadrados (cm²). El área nos indica cuánto espacio ocupa una figura en dos dimensiones.
– Perímetro: Es la suma de las longitudes de todos los lados de una figura. Se expresa en unidades lineales, como metros (m) o centímetros (cm). El perímetro nos da una idea de la distancia alrededor de la figura.
– Volumen: Es la cantidad de espacio que ocupa un objeto tridimensional. Se mide en unidades cúbicas, como metros cúbicos (m³) o centímetros cúbicos (cm³). El volumen es fundamental para entender la capacidad de un objeto.
### 1.2 Importancia en la vida diaria
Los conceptos de área, perímetro y volumen son vitales en diversas situaciones cotidianas. Por ejemplo, al diseñar un jardín, necesitarás calcular el área para determinar cuántas plantas puedes colocar. Si estás construyendo un estanque, el volumen te ayudará a saber cuánta agua necesitarás. Estos cálculos no solo son útiles en la vida personal, sino que también son esenciales en profesiones como la arquitectura, la ingeniería y la planificación urbana.
### 1.3 Un vistazo a las fórmulas
A lo largo de esta guía, exploraremos fórmulas específicas para varias figuras geométricas. Algunas de las más comunes incluyen:
– Área de un rectángulo: ( A = base times altura )
– Perímetro de un rectángulo: ( P = 2 times (base + altura) )
– Volumen de un cubo: ( V = lado^3 )
Conocer estas fórmulas es el primer paso para aplicar los conceptos en situaciones prácticas.
## 2. Cálculo del Área
### 2.1 Fórmulas para figuras planas
El área es una medida clave en geometría, y cada figura tiene su propia fórmula. Aquí te presentamos algunas de las más comunes:
– Cuadrado: ( A = lado^2 )
– Rectángulo: ( A = base times altura )
– Triángulo: ( A = frac{base times altura}{2} )
– Círculo: ( A = pi times radio^2 )
#### Ejemplo práctico
Imagina que deseas colocar césped en tu jardín que tiene forma de rectángulo. Si el jardín mide 10 metros de largo y 5 metros de ancho, puedes calcular el área de la siguiente manera:
[
A = base times altura = 10 , m times 5 , m = 50 , m²
]
Esto significa que necesitarás césped para cubrir 50 metros cuadrados.
### 2.2 Aplicaciones del cálculo de áreas
El cálculo de áreas se utiliza en múltiples campos, como la arquitectura, donde los arquitectos deben conocer el área de los espacios para optimizar el diseño. También es crucial en la agricultura, donde se necesita calcular el área de los cultivos para estimar la producción.
Además, en proyectos de construcción, conocer el área es fundamental para calcular materiales, como pintura o azulejos, que cubren superficies.
## 3. Cálculo del Perímetro
### 3.1 Fórmulas para figuras planas
El perímetro es esencial para medir la longitud total alrededor de una figura. Aquí tienes las fórmulas para las figuras más comunes:
– Cuadrado: ( P = 4 times lado )
– Rectángulo: ( P = 2 times (base + altura) )
– Triángulo: ( P = lado1 + lado2 + lado3 )
– Círculo (también conocido como circunferencia): ( P = 2 times pi times radio )
#### Ejemplo práctico
Supongamos que tienes un jardín en forma de cuadrado con lados de 4 metros. Para calcular el perímetro, aplicarías la fórmula:
[
P = 4 times lado = 4 times 4 , m = 16 , m
]
Esto significa que necesitarás 16 metros de valla para cercar tu jardín.
### 3.2 Importancia del cálculo de perímetros
El cálculo de perímetros es fundamental en la construcción, donde se deben medir las longitudes de los muros y cercas. También es crucial en la planificación de espacios, ya que ayuda a determinar cuántos materiales son necesarios para cercar o dividir áreas.
Además, el perímetro puede ser relevante en deportes, donde las medidas del campo o la pista son esenciales para el diseño y la regulación de las competiciones.
## 4. Cálculo del Volumen
### 4.1 Fórmulas para figuras tridimensionales
El volumen es crucial para entender la capacidad de los objetos. Aquí te presentamos las fórmulas para algunos sólidos más comunes:
– Cubo: ( V = lado^3 )
– Prisma rectangular: ( V = base times altura times profundidad )
– Cilindro: ( V = pi times radio^2 times altura )
– Esfera: ( V = frac{4}{3} times pi times radio^3 )
#### Ejemplo práctico
Si tienes un cubo que mide 3 metros de lado, el volumen se calcularía así:
[
V = lado^3 = 3 , m times 3 , m times 3 , m = 27 , m³
]
Esto significa que el cubo puede contener 27 metros cúbicos de material.
### 4.2 Aplicaciones del cálculo de volúmenes
El cálculo de volúmenes es esencial en muchas industrias. Por ejemplo, en la construcción, se necesita saber el volumen de hormigón para cimientos o estructuras. En la cocina, al medir ingredientes, el volumen ayuda a seguir recetas correctamente.
Además, en la industria del agua, conocer el volumen de tanques y cisternas es crucial para la gestión de recursos hídricos.
## 5. Comparativa entre áreas, perímetros y volúmenes
### 5.1 Diferencias clave
Aunque área, perímetro y volumen son conceptos relacionados, cada uno tiene su propia función:
– Área se refiere a la superficie ocupada por un objeto.
– Perímetro es la longitud total alrededor de un objeto.
– Volumen es la cantidad de espacio que ocupa un objeto tridimensional.
### 5.2 Ejemplos de uso en la vida real
En la vida diaria, es común encontrar situaciones donde se deben calcular estos tres aspectos. Por ejemplo, al diseñar una piscina:
– Área: Se calcula para determinar cuántos metros cuadrados de azulejos se necesitan.
– Perímetro: Se utiliza para medir la longitud de la valla que rodeará la piscina.
– Volumen: Se calcula para saber cuántos litros de agua se requieren para llenarla.
Entender cómo interactúan estas medidas puede ayudarte a abordar problemas prácticos de manera más efectiva.
## 6. Preguntas Frecuentes (FAQ)
### ¿Cuál es la diferencia entre área y superficie?
El término «área» se refiere específicamente a la medida de una superficie en unidades cuadradas, mientras que «superficie» puede referirse a la parte exterior de un objeto en general. En matemáticas, se suele usar «área» para describir la medida de figuras planas.
### ¿Cómo se puede calcular el área de figuras irregulares?
Para calcular el área de figuras irregulares, puedes dividir la figura en partes más simples (como triángulos y rectángulos), calcular el área de cada parte y luego sumarlas. Otra opción es utilizar métodos de aproximación o herramientas como la cuadrícula para estimar el área.
### ¿Qué unidades se utilizan para medir el volumen?
El volumen se mide en unidades cúbicas, como metros cúbicos (m³), litros (L) o centímetros cúbicos (cm³). La elección de la unidad depende del contexto en que se esté trabajando, como en la construcción o en la cocina.
### ¿Por qué es importante conocer el perímetro de una figura?
Conocer el perímetro es importante para diversas aplicaciones prácticas, como la construcción de cercas, el diseño de jardines y la planificación de espacios. También se utiliza en deportes para medir campos y pistas.
### ¿Cómo se relacionan área, perímetro y volumen en un objeto tridimensional?
En un objeto tridimensional, el área se refiere a las superficies de sus caras, el perímetro se relaciona con las longitudes de sus bordes y el volumen mide el espacio interno. Comprender esta relación es fundamental para resolver problemas complejos en geometría.
### ¿Puedo calcular el área de un círculo sin conocer el radio?
Sí, si conoces el diámetro del círculo, puedes calcular el radio dividiendo el diámetro entre 2. Luego, puedes aplicar la fórmula del área ( A = pi times radio^2 ).
### ¿Existen calculadoras en línea para áreas, perímetros y volúmenes?
Sí, hay muchas calculadoras en línea que te permiten calcular áreas, perímetros y volúmenes de diversas figuras geométricas. Estas herramientas son muy útiles para verificar tus cálculos o para aprender a aplicar las fórmulas correctas.