Descubre la Fórmula del Perímetro de un Triángulo Rectángulo: Guía Completa
¿Alguna vez te has preguntado cómo calcular el perímetro de un triángulo rectángulo? Este concepto, fundamental en la geometría, es esencial no solo para estudiantes, sino también para quienes trabajan en campos que requieren mediciones precisas. En esta guía, vamos a desglosar la fórmula del perímetro de un triángulo rectángulo, explorando sus componentes, aplicaciones y ejemplos prácticos. Aprenderás no solo la fórmula básica, sino también cómo aplicarla en diversas situaciones, lo que te permitirá mejorar tu comprensión de la geometría y su relevancia en la vida diaria. Prepárate para descubrir todo lo que necesitas saber sobre el perímetro de un triángulo rectángulo y cómo calcularlo de manera efectiva.
¿Qué es un Triángulo Rectángulo?
Un triángulo rectángulo es un tipo de triángulo que tiene un ángulo de 90 grados. Esta característica lo distingue de otros triángulos, ya que los otros dos ángulos son siempre agudos. Esta forma geométrica es fundamental en la matemática y la física, y se encuentra en muchas aplicaciones prácticas, desde la arquitectura hasta la ingeniería.
Características de un Triángulo Rectángulo
Los triángulos rectángulos tienen varias características que los hacen únicos:
- Hipotenusa: Es el lado opuesto al ángulo recto y el más largo del triángulo.
- Catetos: Son los otros dos lados que forman el ángulo recto. Estos lados son perpendiculares entre sí.
- Relaciones Trigonométricas: En un triángulo rectángulo, se pueden aplicar funciones trigonométricas como el seno, coseno y tangente, que son fundamentales en el estudio de las matemáticas.
Estas características son clave para entender no solo el perímetro, sino también otras propiedades y fórmulas relacionadas con los triángulos rectángulos.
Ejemplos de Triángulos Rectángulos en la Vida Real
Los triángulos rectángulos se pueden encontrar en diversas situaciones cotidianas, como:
- Escaleras apoyadas contra una pared, donde la escalera es la hipotenusa.
- Triángulos formados por la estructura de techos en edificios.
- El diseño de rampas de acceso, donde se utilizan triángulos rectángulos para garantizar la seguridad y la funcionalidad.
Estas aplicaciones demuestran la importancia de comprender cómo funcionan los triángulos rectángulos, especialmente cuando se trata de cálculos precisos como el perímetro.
La Fórmula del Perímetro de un Triángulo Rectángulo
El perímetro de un triángulo se define como la suma de la longitud de todos sus lados. En el caso de un triángulo rectángulo, la fórmula para calcular el perímetro es bastante sencilla:
Perímetro (P) = Cateto 1 + Cateto 2 + Hipotenusa
Para poder aplicar esta fórmula, es necesario conocer las longitudes de los dos catetos y la hipotenusa. A continuación, exploraremos cada uno de estos componentes.
Identificando los Lados del Triángulo
Para calcular el perímetro, primero debes identificar los lados del triángulo:
- Cateto 1 (a): Uno de los lados que forma el ángulo recto.
- Cateto 2 (b): El otro lado que forma el ángulo recto.
- Hipotenusa (c): El lado más largo, opuesto al ángulo recto.
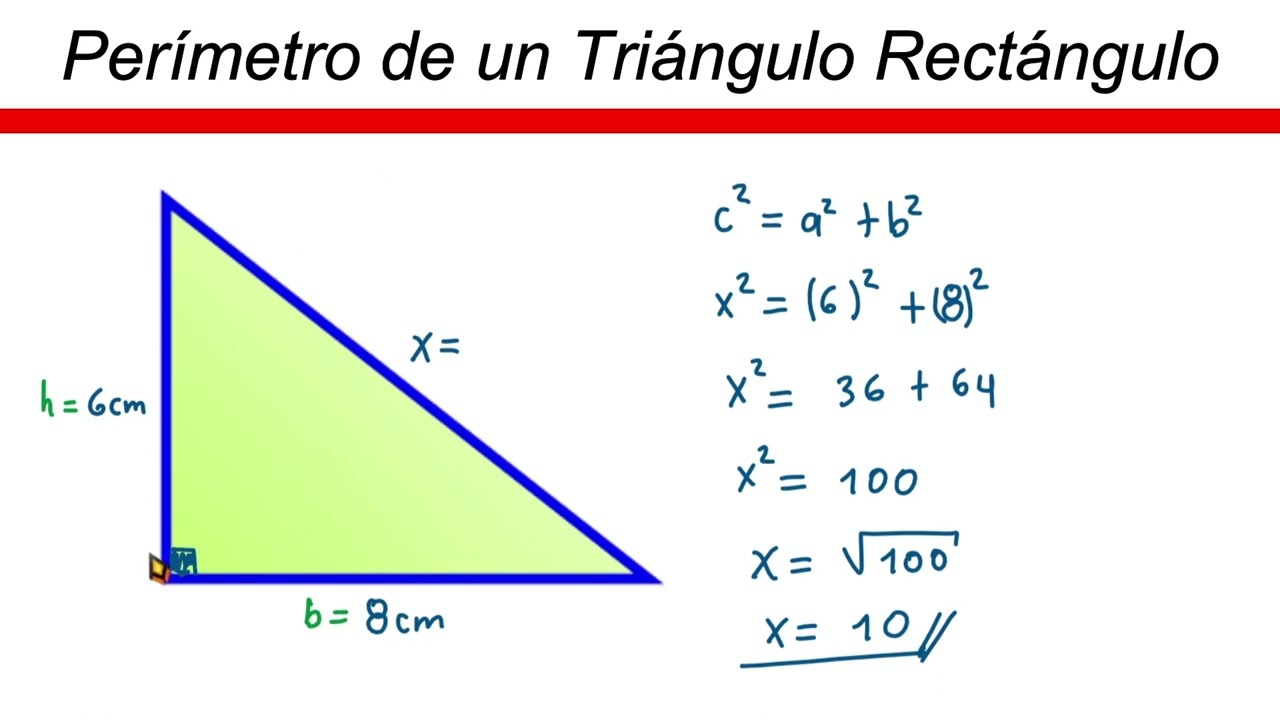
Si solo conoces los catetos, puedes calcular la hipotenusa utilizando el Teorema de Pitágoras:
c = √(a² + b²)
Ejemplo Práctico de Cálculo del Perímetro
Supongamos que tenemos un triángulo rectángulo donde los catetos miden 3 cm y 4 cm. Primero, calculamos la hipotenusa:
c = √(3² + 4²) = √(9 + 16) = √25 = 5 cm
Ahora, aplicamos la fórmula del perímetro:
P = 3 cm + 4 cm + 5 cm = 12 cm
Así, el perímetro del triángulo rectángulo es de 12 cm. Este método puede aplicarse a cualquier triángulo rectángulo siempre que se conozcan las longitudes de los lados.
Aplicaciones del Perímetro de un Triángulo Rectángulo
El cálculo del perímetro de un triángulo rectángulo tiene varias aplicaciones en la vida real, desde proyectos de construcción hasta el diseño gráfico. Conocer el perímetro es esencial para:
- Diseño Arquitectónico: Los arquitectos utilizan triángulos rectángulos para garantizar la estabilidad y la estética de sus construcciones.
- Medición de Espacios: En la planificación de interiores, el perímetro se utiliza para calcular la cantidad de materiales necesarios, como pintura o alfombra.
- Ingeniería: En campos como la ingeniería civil, el cálculo del perímetro es crucial para el diseño de estructuras y caminos.
Además, el perímetro también se utiliza en deportes y actividades recreativas. Por ejemplo, al diseñar un campo de juego o una pista de atletismo, se requieren cálculos precisos para asegurar que las dimensiones sean adecuadas y seguras.
El Perímetro en Proyectos de Construcción
En el ámbito de la construcción, el perímetro es fundamental para determinar el tamaño y la forma de los cimientos. Un cálculo incorrecto puede llevar a problemas de estabilidad, lo que subraya la importancia de comprender cómo calcularlo. Por ejemplo, si un contratista está diseñando una plataforma para una casa, necesita conocer el perímetro para asegurar que el espacio sea suficiente para soportar la estructura.
El Perímetro en el Diseño Gráfico
En el diseño gráfico, los triángulos rectángulos son comunes en la creación de elementos visuales. Los diseñadores a menudo utilizan estos triángulos para crear composiciones equilibradas y estéticamente agradables. Comprender el perímetro de estos triángulos permite a los diseñadores calcular el espacio necesario para sus elementos, asegurando que todo encaje de manera adecuada en el diseño final.
Errores Comunes al Calcular el Perímetro
Al calcular el perímetro de un triángulo rectángulo, es fácil cometer errores. Algunos de los más comunes incluyen:
- No identificar correctamente los lados: Asegúrate de saber cuál es la hipotenusa y cuáles son los catetos.
- Confundir las unidades de medida: Siempre verifica que todas las medidas estén en la misma unidad antes de calcular.
- Olvidar aplicar el Teorema de Pitágoras: Si no conoces la hipotenusa, asegúrate de calcularla correctamente.
Estos errores pueden llevar a resultados inexactos, así que es importante prestar atención a cada paso del proceso de cálculo. Practicar con diferentes ejemplos puede ayudar a evitar estos problemas en el futuro.
Preguntas Frecuentes (FAQ)
¿Cuál es la diferencia entre el perímetro y el área de un triángulo rectángulo?
El perímetro se refiere a la suma de todos los lados del triángulo, mientras que el área es la medida de la superficie encerrada dentro del triángulo. Para calcular el área de un triángulo rectángulo, se utiliza la fórmula: Área = (base x altura) / 2. Por lo tanto, mientras que el perímetro se centra en la longitud de los lados, el área se ocupa del espacio que ocupa el triángulo.
¿Puedo usar la fórmula del perímetro para otros tipos de triángulos?
Sí, la fórmula del perímetro se puede aplicar a cualquier tipo de triángulo, ya sea equilátero, isósceles o escaleno. Sin embargo, la manera de determinar las longitudes de los lados puede variar. Para triángulos que no son rectángulos, es posible que necesites aplicar otras fórmulas o teoremas, como el Teorema de Herón.
¿Cómo puedo practicar el cálculo del perímetro de triángulos rectángulos?
Una excelente manera de practicar es resolver problemas de ejercicios que incluyan diferentes triángulos rectángulos. Puedes buscar libros de texto de geometría, sitios web educativos o incluso aplicaciones móviles que ofrezcan problemas de práctica. Asegúrate de variar los problemas, incluyendo triángulos con diferentes medidas y condiciones.
¿Qué aplicaciones prácticas tiene el cálculo del perímetro en la vida cotidiana?
El cálculo del perímetro tiene múltiples aplicaciones en la vida diaria, como en la construcción, el diseño de interiores, la planificación de jardines y la creación de espacios recreativos. Por ejemplo, al instalar una cerca, es necesario calcular el perímetro del área que deseas cercar para determinar cuántos materiales necesitarás.
¿Es necesario saber trigonometría para calcular el perímetro de un triángulo rectángulo?
No es estrictamente necesario conocer trigonometría para calcular el perímetro de un triángulo rectángulo, pero entender conceptos básicos de trigonometría puede ser útil, especialmente si necesitas calcular la hipotenusa. Sin embargo, si tienes las longitudes de los catetos, puedes calcular el perímetro directamente sin aplicar trigonometría.
¿Qué herramientas puedo usar para calcular el perímetro?
Para calcular el perímetro de un triángulo rectángulo, puedes usar una calculadora básica para realizar operaciones matemáticas simples. También puedes utilizar software de diseño o aplicaciones de geometría que faciliten el cálculo y la visualización de triángulos. Por último, el uso de papel y lápiz para realizar cálculos manuales también es una opción efectiva.