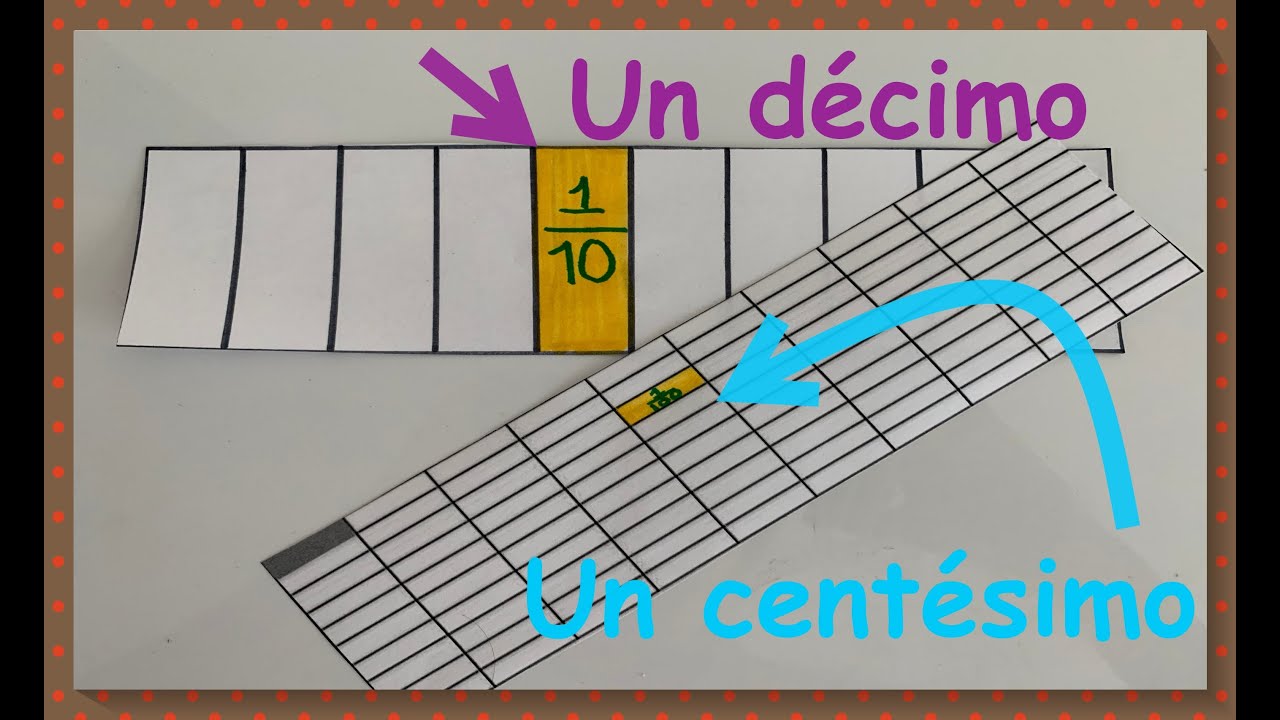
¿Cuántos milésimos caben en un décimo? Descubre la respuesta aquí

Si alguna vez te has preguntado ¿cuántos milésimos caben en un décimo?, no estás solo. Esta es una consulta común que puede surgir en diversas áreas, desde la educación matemática hasta la vida cotidiana. Entender la relación entre milésimos y décimos es esencial, no solo para resolver problemas matemáticos, sino también para aplicar conceptos de medición y proporción en situaciones reales. En este artículo, exploraremos a fondo esta relación, desglosando conceptos básicos y ofreciendo ejemplos claros que te ayudarán a asimilar la información de manera efectiva.

A lo largo de este artículo, descubrirás qué son los décimos y los milésimos, cómo se relacionan entre sí, y aprenderás a realizar conversiones entre estas dos unidades. Además, abordaremos ejemplos prácticos que ilustran su uso en la vida diaria. Al final, tendrás una comprensión sólida de cómo se entrelazan estos conceptos y cómo puedes aplicarlos en diferentes contextos. ¡Vamos a sumergirnos en el fascinante mundo de los números!

¿Qué son los décimos?

Los décimos son una unidad de medida que representa una parte de diez. En el sistema decimal, el décimo se simboliza como 0.1. Esto significa que cuando dividimos una unidad en diez partes iguales, cada una de esas partes es un décimo. Los décimos son fundamentales en diversas aplicaciones, desde la matemática básica hasta el uso en finanzas y mediciones.

Ejemplos de décimos en la vida cotidiana

Los décimos se encuentran en situaciones cotidianas. Por ejemplo:

• Dinero: Si tienes un billete de un euro y lo divides en diez partes, cada parte representaría diez céntimos, que es un décimo de euro.
• Calificaciones: En un sistema de calificación de 10 puntos, una calificación de 7.5 sería equivalente a 7 décimos y medio.

Estos ejemplos muestran cómo los décimos son una forma práctica de expresar fracciones y cantidades en diferentes contextos. Comprender esta unidad te ayudará a realizar cálculos más precisos en tu vida diaria.

¿Qué son los milésimos?

Los milésimos, por otro lado, representan una parte de mil. En el sistema decimal, un milésimo se simboliza como 0.001. Esto significa que cuando dividimos una unidad en mil partes iguales, cada una de esas partes es un milésimo. Al igual que los décimos, los milésimos son importantes en diversas áreas, como la ciencia, la ingeniería y las finanzas.

Ejemplos de milésimos en la vida cotidiana

Los milésimos también se pueden observar en situaciones cotidianas. Algunos ejemplos incluyen:

• Mediciones de precisión: En la ciencia, las mediciones a menudo se expresan en milésimos, como en la temperatura o la longitud.
• Finanzas: En transacciones monetarias, especialmente en el ámbito de los intereses, los milésimos pueden representar tasas de interés muy pequeñas.

Estos ejemplos ilustran cómo los milésimos son esenciales para una comprensión precisa en contextos donde se requiere un alto grado de exactitud.

Relación entre décimos y milésimos

Ahora que hemos definido los décimos y los milésimos, es hora de abordar la pregunta principal: ¿cuántos milésimos caben en un décimo? La respuesta es bastante sencilla: hay 100 milésimos en un décimo. Esto se debe a que un décimo (0.1) se puede expresar como 100 milésimos (0.001 x 100 = 0.1).

Ejemplo práctico de conversión

Para ilustrar esta relación, considera el siguiente ejemplo:

• Si tienes 3 décimos, ¿cuántos milésimos son? Multiplicamos 3 décimos por 100 milésimos por décimo:
• 3 décimos x 100 milésimos/décimo = 300 milésimos.

Así, puedes ver que la conversión entre décimos y milésimos es directa y fácil de manejar una vez que entiendes la relación. Este conocimiento es útil en diversas situaciones, desde cálculos matemáticos hasta aplicaciones prácticas en la vida diaria.

Cálculos con décimos y milésimos

Los cálculos que involucran décimos y milésimos pueden ser esenciales en una variedad de contextos. Aquí, exploraremos algunos de los cálculos más comunes que puedes realizar utilizando estas unidades.

Sumas y restas

Las operaciones de suma y resta son fundamentales cuando trabajamos con décimos y milésimos. Por ejemplo, si deseas sumar 0.1 (un décimo) y 0.001 (un milésimo), debes convertir ambos números a la misma unidad. En este caso, puedes convertir el décimo a milésimos:

• 0.1 = 100 milésimos
• Entonces, 100 milésimos + 1 milésimo = 101 milésimos.

Por lo tanto, la suma de 0.1 y 0.001 es igual a 0.101. Este tipo de conversión es clave para realizar cálculos precisos.

Multiplicaciones y divisiones

Las multiplicaciones y divisiones también son comunes. Por ejemplo, si multiplicas 0.1 por 10, obtienes 1. Sin embargo, si trabajas con milésimos y deseas saber cuántos milésimos hay en 0.1, puedes usar la relación que discutimos anteriormente:

• 0.1 x 1000 = 100 milésimos.

Esto demuestra cómo las operaciones pueden variar según la unidad que estés utilizando. La clave es siempre recordar la relación entre las unidades.

Aplicaciones prácticas en diferentes campos

La comprensión de la relación entre décimos y milésimos tiene aplicaciones en diversos campos, desde la educación hasta la industria. Aquí exploraremos algunas de estas aplicaciones prácticas.

En educación matemática

En el ámbito educativo, la enseñanza de décimos y milésimos es fundamental para que los estudiantes desarrollen habilidades numéricas sólidas. Los maestros utilizan estas unidades para enseñar conceptos de fracciones, proporciones y decimales, facilitando la comprensión de las relaciones numéricas. Las actividades prácticas, como medir objetos o realizar experimentos, permiten a los estudiantes ver la relevancia de estos conceptos en la vida real.

En ingeniería y ciencia

En campos como la ingeniería y la ciencia, los milésimos son cruciales para realizar mediciones precisas. Por ejemplo, en la fabricación de componentes mecánicos, se requiere una precisión milimétrica. La comprensión de las relaciones entre décimos y milésimos permite a los ingenieros realizar cálculos precisos y garantizar que los componentes encajen correctamente. Esto es vital para la seguridad y la eficacia de las estructuras y dispositivos que diseñan.

FAQ (Preguntas Frecuentes)

1. ¿Qué es un décimo en términos de fracciones?

Un décimo es una fracción que representa una parte de diez, es decir, 1/10. En el sistema decimal, se expresa como 0.1. Es fundamental para entender la división de una unidad en diez partes iguales, y se utiliza frecuentemente en matemáticas y situaciones cotidianas.

2. ¿Cómo se convierte un décimo en milésimos?

Para convertir un décimo a milésimos, simplemente multiplicas el número de décimos por 100, ya que un décimo equivale a 100 milésimos. Por ejemplo, 0.2 (dos décimos) sería igual a 200 milésimos (0.2 x 100 = 200).

3. ¿Por qué son importantes los milésimos en la ciencia?

Los milésimos son esenciales en la ciencia porque permiten realizar mediciones muy precisas. En campos como la química, la física y la ingeniería, donde los resultados dependen de la exactitud, utilizar milésimos asegura que los experimentos y cálculos se realicen de manera correcta y confiable.

4. ¿Cómo se utilizan décimos y milésimos en el ámbito financiero?

En finanzas, los décimos y milésimos se utilizan para expresar tasas de interés y otros valores monetarios. Por ejemplo, un interés del 0.5% se puede representar como cinco décimos de un por ciento, mientras que un interés de 0.001 sería un milésimo de un por ciento. Esto es fundamental para realizar cálculos financieros precisos.

5. ¿Es posible trabajar con décimos y milésimos en cálculos complejos?

Sí, es posible. Los décimos y milésimos se utilizan frecuentemente en cálculos complejos en matemáticas, física y economía. La clave es tener una comprensión clara de cómo convertir entre estas unidades y aplicar correctamente las operaciones matemáticas.

6. ¿Puedo usar décimos y milésimos en programación?

Absolutamente. En programación, los décimos y milésimos se utilizan para representar datos numéricos con precisión. Las funciones matemáticas en muchos lenguajes de programación permiten realizar operaciones con decimales, lo que facilita la manipulación de estas unidades en cálculos y algoritmos.

7. ¿Qué errores comunes se cometen al trabajar con décimos y milésimos?

Un error común es no convertir correctamente entre las unidades, lo que puede llevar a resultados inexactos. También, al sumar o restar, algunas personas olvidan alinear los decimales. Es fundamental prestar atención a estas conversiones y operaciones para evitar confusiones y errores en los cálculos.