¿Cuál es el Denominador de una Fracción? Guía Completa y Ejemplos Explicativos

Las fracciones son un concepto fundamental en matemáticas, y entender sus componentes es clave para manejar operaciones matemáticas con eficacia. Uno de los elementos más importantes de una fracción es el denominador, que a menudo puede generar confusión entre estudiantes y personas que se inician en el aprendizaje de esta área. ¿Te has preguntado alguna vez qué es exactamente el denominador y por qué es tan relevante? En esta guía completa, exploraremos en detalle qué es el denominador de una fracción, cómo se utiliza y su importancia en el contexto de las matemáticas. Además, incluiremos ejemplos prácticos que te ayudarán a visualizar y comprender mejor este concepto. Prepárate para sumergirte en el fascinante mundo de las fracciones y dominar el conocimiento sobre el denominador.

¿Qué es una Fracción?

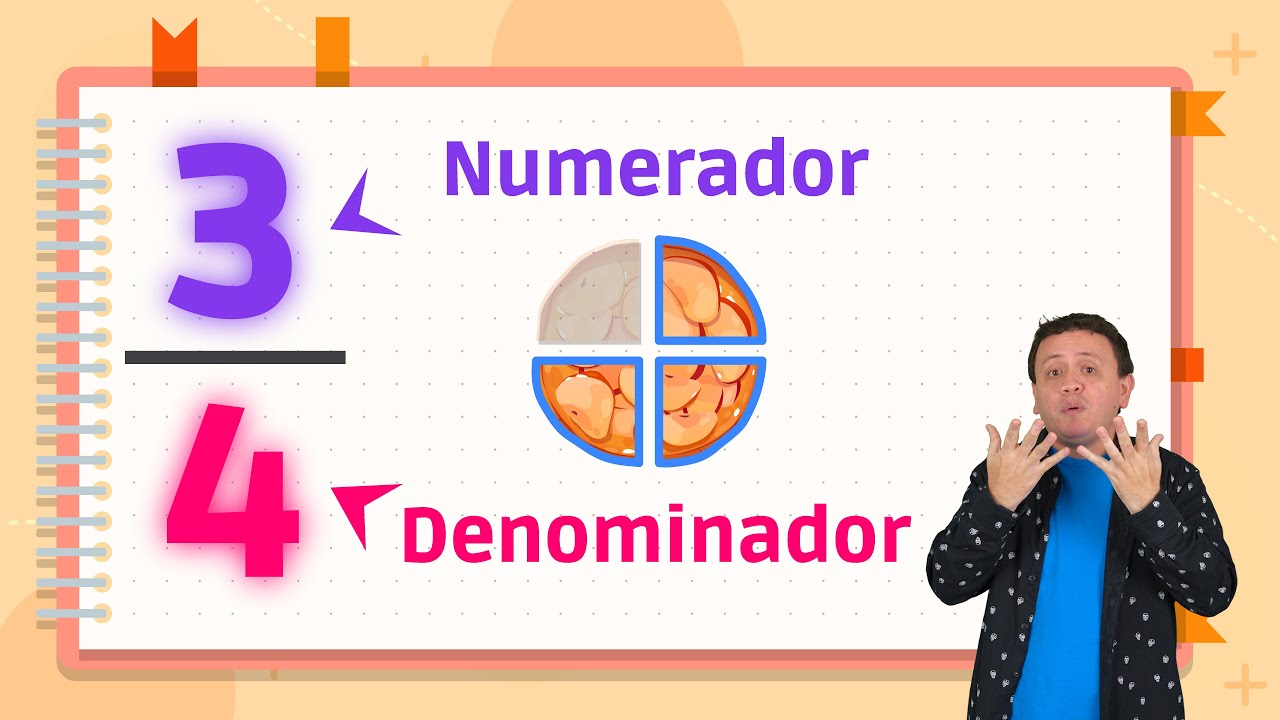
Para comprender el denominador, primero debemos definir qué es una fracción. Una fracción es una representación numérica que expresa la división de dos cantidades: el numerador y el denominador. El numerador se encuentra en la parte superior de la fracción y representa la cantidad que se está considerando, mientras que el denominador, que se sitúa en la parte inferior, indica en cuántas partes iguales se ha dividido la unidad total.

Componentes de una Fracción

Las fracciones están compuestas por dos partes principales:

• Numerador: Es el número que se encuentra arriba y que indica cuántas partes de un todo estamos considerando.
• Denominador: Es el número que se encuentra abajo y que muestra en cuántas partes iguales se ha dividido el total.

Por ejemplo, en la fracción ¾, el 3 es el numerador y el 4 es el denominador. Esto significa que hemos dividido algo en 4 partes iguales y estamos considerando 3 de esas partes.

Tipos de Fracciones

Existen diferentes tipos de fracciones que se clasifican según la relación entre el numerador y el denominador:

• Fracciones propias: El numerador es menor que el denominador (ejemplo: ⅗).
• Fracciones impropias: El numerador es mayor o igual que el denominador (ejemplo: 5/4).
• Fracciones mixtas: Combinan un número entero y una fracción propia (ejemplo: 1 ½).

Entender estos tipos de fracciones es fundamental para trabajar con el denominador, ya que la naturaleza de la fracción influye en cómo se realizan las operaciones matemáticas.

¿Cuál es el Rol del Denominador en una Fracción?

El denominador desempeña un papel crucial en la interpretación y operación de las fracciones. En términos simples, determina cuántas partes iguales hay en el todo. Esto no solo es importante para entender la fracción en sí, sino también para realizar operaciones matemáticas como la suma, resta, multiplicación y división de fracciones.

Ejemplo de la Importancia del Denominador

Imagina que tienes una pizza que ha sido dividida en 8 partes iguales. Si comes 3 porciones, la fracción que representa lo que has comido es 3/8. Aquí, el 8 (denominador) es fundamental, ya que nos indica cuántas partes hay en total. Si la pizza se hubiera dividido en 4 partes, y hubieras comido 3, la fracción sería 3/4, lo que representa una cantidad diferente de pizza. Esto demuestra cómo el denominador afecta la magnitud de la fracción y, por lo tanto, su interpretación.

Denominador y Operaciones Matemáticas

Las operaciones con fracciones requieren que se preste especial atención al denominador. Por ejemplo:

• Suma de fracciones: Para sumar fracciones con diferentes denominadores, es necesario encontrar un denominador común.
• Multiplicación de fracciones: Aquí, multiplicamos los numeradores y los denominadores de forma independiente, lo que puede resultar en un denominador mayor o menor dependiendo de los números involucrados.
• División de fracciones: Invertimos la segunda fracción y multiplicamos, lo que también puede cambiar el denominador.

Por lo tanto, el denominador no solo ayuda a definir la fracción, sino que también guía cómo se manejan las operaciones matemáticas con ella.

Cómo Identificar el Denominador en Diferentes Fracciones

Identificar el denominador es esencial para trabajar con fracciones. A continuación, exploraremos cómo se puede hacer esto en diferentes contextos.

Fracciones Simples

Las fracciones simples son aquellas que tienen un numerador y un denominador. Para identificarlas, simplemente mira la fracción y observa el número en la parte inferior. Por ejemplo, en 2/5, el denominador es 5.

Fracciones Complejas

Las fracciones complejas son aquellas que contienen fracciones en el numerador, el denominador o en ambos. Por ejemplo, en la fracción (1/2)/(3/4), el denominador de la fracción completa es 3/4. Identificar el denominador en este caso implica reconocer que se está trabajando con una fracción dentro de otra fracción.

Fracciones en Contextos de Problemas Reales

En situaciones del mundo real, como recetas de cocina o medidas en construcción, es común encontrar fracciones. Aquí, el denominador puede representar diferentes cosas. Por ejemplo, si en una receta se indica que necesitas ¾ de taza de azúcar, el denominador (4) sugiere que el total de la medida se ha dividido en 4 partes iguales. Esto ayuda a entender cómo ajustar las cantidades según el número de porciones que se deseen.

Ejemplos Prácticos del Uso del Denominador

Ver ejemplos prácticos puede ayudar a solidificar el entendimiento del denominador. Vamos a ver algunos casos específicos donde el denominador juega un papel importante.

Ejemplo 1: Suma de Fracciones

Supongamos que queremos sumar 1/4 y 1/6. Para hacer esto, necesitamos un denominador común. El mínimo común múltiplo de 4 y 6 es 12. Entonces, convertimos las fracciones:

• 1/4 = 3/12 (multiplicamos por 3)
• 1/6 = 2/12 (multiplicamos por 2)

Ahora podemos sumarlas: 3/12 + 2/12 = 5/12.

Ejemplo 2: Multiplicación de Fracciones

Multiplicando 2/3 por 4/5, simplemente multiplicamos los numeradores y denominadores:

• Numerador: 2 x 4 = 8
• Denominador: 3 x 5 = 15

Por lo tanto, 2/3 x 4/5 = 8/15.

Ejemplo 3: Fracciones en Contextos Reales

Imagina que estás cocinando y necesitas 2/3 de taza de harina. Si decides hacer solo la mitad de la receta, ¿cuánto necesitas? Simplemente multiplicas el denominador por 2 (2/3 x 1/2 = 2/6 = 1/3). Aquí, el denominador te ayuda a ajustar las cantidades de forma efectiva.

Preguntas Frecuentes (FAQ)

1. ¿Por qué es importante el denominador en las fracciones?

El denominador es fundamental porque determina cuántas partes iguales hay en el todo. Sin un denominador, no podríamos entender la proporción que representa la fracción. Además, es crucial para realizar operaciones matemáticas como suma, resta, multiplicación y división de fracciones.

2. ¿Cómo se encuentra el denominador común para sumar fracciones?

Para encontrar el denominador común, primero identifica los denominadores de las fracciones que deseas sumar. Luego, busca el mínimo común múltiplo (MCM) de esos denominadores. Una vez que tengas el MCM, convierte cada fracción para que tenga este nuevo denominador, y luego podrás sumarlas.

3. ¿Qué sucede si el denominador es cero?

Un denominador no puede ser cero porque no se puede dividir entre cero. Esto resultaría en una indeterminación en matemáticas. Si encuentras una fracción con un denominador de cero, es un caso inválido y no se puede calcular.

4. ¿Cómo se simplifican las fracciones y qué papel juega el denominador?

Para simplificar una fracción, divide tanto el numerador como el denominador por su máximo común divisor (MCD). El denominador juega un papel crucial en este proceso, ya que determina el tamaño de la fracción simplificada. Por ejemplo, en 4/8, el MCD es 4, por lo que al simplificar obtenemos 1/2.

5. ¿Se pueden tener denominadores negativos en las fracciones?

Sí, se pueden tener denominadores negativos en fracciones. Sin embargo, es común convertir el denominador negativo en positivo, cambiando el signo del numerador. Por ejemplo, -3/4 se puede escribir como 3/-4. Ambos representan la misma cantidad, pero se prefiere el uso de denominadores positivos por razones de claridad.

6. ¿Cómo afectan los denominadores en las fracciones impropias?

En las fracciones impropias, donde el numerador es mayor o igual que el denominador, el denominador aún cumple su función de mostrar cuántas partes iguales hay en el total. Sin embargo, en este caso, la fracción puede ser convertida en un número mixto, lo que ayuda a visualizar mejor la cantidad representada.

7. ¿Qué son los denominadores equivalentes?

Los denominadores equivalentes son diferentes denominadores que representan la misma cantidad. Por ejemplo, 1/2 y 2/4 son fracciones equivalentes porque ambas representan la misma parte del total. El denominador es diferente, pero el valor de la fracción sigue siendo el mismo. Esto es útil al sumar o comparar fracciones.