Cómo Hallar el Perímetro de un Polígono: Guía Paso a Paso y Ejemplos Prácticos

Calcular el perímetro de un polígono es una habilidad fundamental en matemáticas, útil en diversas aplicaciones cotidianas, desde la construcción hasta el diseño gráfico. El perímetro se refiere a la suma de todos los lados de una figura, y aunque puede parecer un concepto sencillo, entenderlo completamente te permitirá abordar problemas más complejos con confianza. En este artículo, exploraremos cómo hallar el perímetro de diferentes tipos de polígonos, desde los más simples, como el triángulo, hasta los más complejos, como los polígonos irregulares. A lo largo de esta guía, encontrarás ejemplos prácticos y consejos útiles que facilitarán tu aprendizaje. Prepárate para convertirte en un experto en el cálculo de perímetros, mientras desglosamos el proceso paso a paso.

1. ¿Qué es el Perímetro y por qué es Importante?

El perímetro es la distancia total alrededor de un polígono. Imagina que estás rodeando un campo; la longitud del camino que recorres es el perímetro de ese campo. Conocer el perímetro es crucial en múltiples contextos. Por ejemplo, si estás planeando una cerca para tu jardín, necesitas saber cuánto material comprar, lo que implica calcular el perímetro del área que deseas cercar. Además, el perímetro es una medida esencial en arquitectura, diseño de interiores y muchas otras disciplinas.

1.1 Definición de Perímetro

En términos simples, el perímetro de un polígono es la suma de la longitud de todos sus lados. Para un triángulo, se suma la longitud de los tres lados; para un cuadrado, se multiplica la longitud de un lado por cuatro. Este concepto se aplica de manera uniforme a cualquier polígono, ya sea regular o irregular.

1.2 Aplicaciones Prácticas del Perímetro

El cálculo del perímetro se utiliza en diversas situaciones cotidianas. Algunos ejemplos incluyen:

• Construcción: Al calcular la cantidad de material necesario para cercas, pisos o paredes.
• Jardinería: Para determinar cuánta tierra o césped se necesita para cubrir un área específica.
• Diseño Gráfico: Para calcular bordes y márgenes en la creación de layouts.

Entender cómo hallar el perímetro no solo es útil, sino que también es una habilidad matemática básica que te ayudará a desarrollar un pensamiento lógico y analítico.

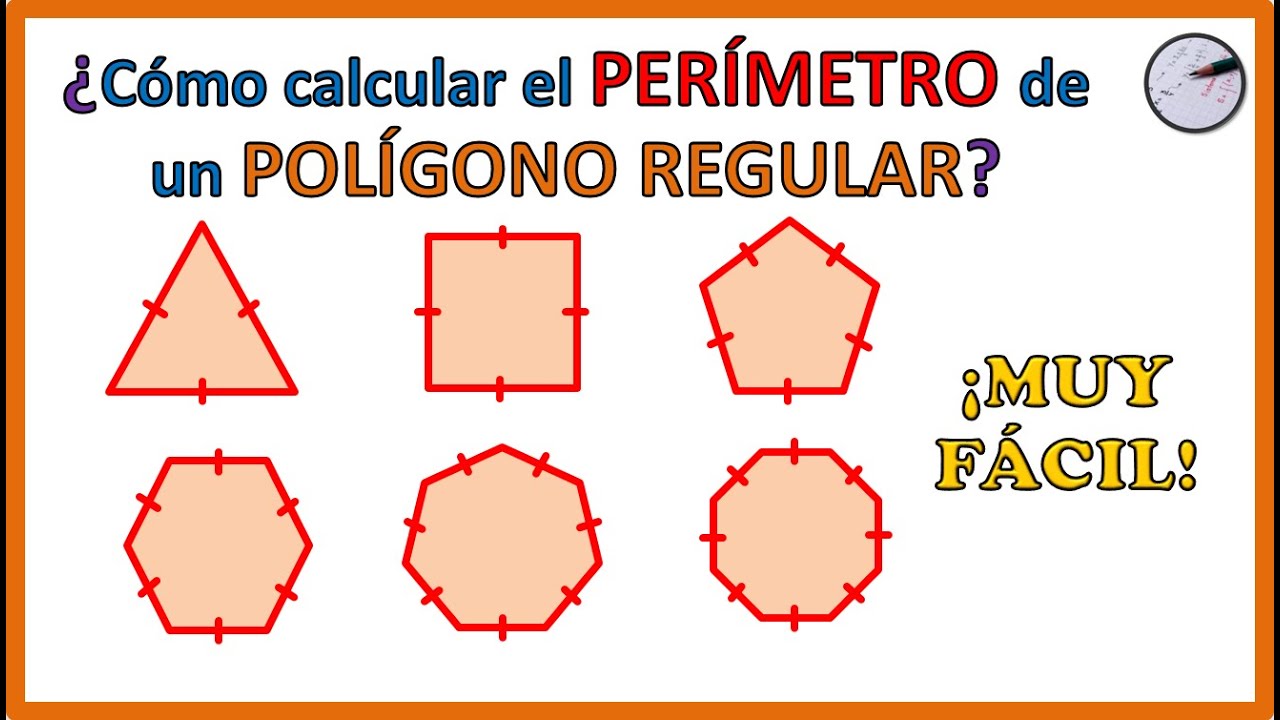
2. Cómo Hallar el Perímetro de Polígonos Regulares

Los polígonos regulares son aquellos que tienen todos sus lados y ángulos iguales. Ejemplos comunes incluyen el cuadrado, el triángulo equilátero y el hexágono regular. Hallar el perímetro de estos polígonos es bastante sencillo, ya que puedes aplicar fórmulas específicas.

2.1 Triángulo Equilátero

Para calcular el perímetro de un triángulo equilátero, simplemente multiplica la longitud de un lado por tres. Si un lado mide 5 cm, el perímetro sería:

Perímetro = 3 × 5 cm = 15 cm

2.2 Cuadrado

El perímetro de un cuadrado se obtiene multiplicando la longitud de un lado por cuatro. Por ejemplo, si un lado mide 4 m, el cálculo sería:

Perímetro = 4 × 4 m = 16 m

2.3 Hexágono Regular

Para un hexágono regular, que tiene seis lados, el perímetro se calcula multiplicando la longitud de un lado por seis. Si un lado mide 2 cm, el perímetro será:

Perímetro = 6 × 2 cm = 12 cm

Estos ejemplos ilustran que hallar el perímetro de polígonos regulares es un proceso directo que se puede aplicar fácilmente con las fórmulas adecuadas.

3. Cómo Hallar el Perímetro de Polígonos Irregulares

A diferencia de los polígonos regulares, los polígonos irregulares tienen lados y ángulos de diferentes longitudes. Para hallar el perímetro de un polígono irregular, simplemente se suman las longitudes de todos sus lados. Este proceso puede parecer más complicado, pero con un enfoque sistemático, se vuelve manejable.

3.1 Sumar Lados Individualmente

Para calcular el perímetro de un polígono irregular, primero mide cada lado. Por ejemplo, supongamos que tienes un pentágono cuyas longitudes de lados son 3 cm, 4 cm, 5 cm, 6 cm y 7 cm. El perímetro se calcularía así:

Perímetro = 3 cm + 4 cm + 5 cm + 6 cm + 7 cm = 25 cm

3.2 Uso de Herramientas de Medición

En algunos casos, especialmente en proyectos más grandes, puede ser útil utilizar herramientas de medición, como cintas métricas o reglas, para obtener longitudes precisas. Esto es especialmente relevante en la construcción o en proyectos de jardinería donde los errores de medición pueden resultar costosos.

3.3 Ejemplo Práctico

Imagina que deseas calcular el perímetro de un terreno con forma irregular. Mides los lados y obtienes las siguientes longitudes: 10 m, 15 m, 12 m, 8 m y 5 m. Al sumar:

Perímetro = 10 m + 15 m + 12 m + 8 m + 5 m = 50 m

Como puedes ver, aunque los polígonos irregulares requieren más pasos, el proceso es igual de directo: simplemente suma las longitudes de todos los lados.

4. Polígonos con Lados de Diferentes Longitudes

Algunos polígonos tienen lados que no son iguales y pueden ser más complejos en su forma. A continuación, analizaremos cómo se puede abordar el cálculo del perímetro en estos casos.

4.1 Identificación de Lados

El primer paso es identificar y medir cada lado del polígono. Para un rectángulo, por ejemplo, los lados opuestos son iguales. Si un rectángulo tiene lados de 6 m y 4 m, los lados son 6 m, 4 m, 6 m y 4 m.

4.2 Fórmulas Específicas para Ciertos Polígonos

En algunos casos, existen fórmulas específicas. Por ejemplo, para un rectángulo, el perímetro se calcula como:

Perímetro = 2 × (largo + ancho)

Si un rectángulo tiene un largo de 8 m y un ancho de 3 m, el cálculo sería:

Perímetro = 2 × (8 m + 3 m) = 22 m

4.3 Ejemplo con un Polígono Irregular

Supongamos que tienes un polígono irregular con lados de 5 m, 7 m, 3 m, 9 m y 4 m. Para hallar el perímetro, simplemente sumas las longitudes:

Perímetro = 5 m + 7 m + 3 m + 9 m + 4 m = 28 m

Este enfoque te permite manejar cualquier polígono con lados de diferentes longitudes de manera efectiva.

5. Errores Comunes al Calcular el Perímetro

Calcular el perímetro puede parecer fácil, pero hay errores comunes que pueden surgir. Identificar y evitar estos errores te ayudará a mejorar tu precisión.

5.1 No Sumar Todos los Lados

Uno de los errores más frecuentes es olvidar sumar todos los lados del polígono. Es fundamental asegurarte de que cada lado sea considerado, especialmente en polígonos irregulares.

5.2 Medidas Incorrectas

La precisión de tus medidas es crucial. Utiliza herramientas adecuadas y verifica tus mediciones antes de realizar el cálculo. Un error de medición puede llevar a un resultado incorrecto.

5.3 No Usar las Fórmulas Adecuadas

Para ciertos polígonos, como los rectángulos o los cuadrados, es más eficiente usar fórmulas específicas en lugar de sumar cada lado. Asegúrate de conocer estas fórmulas para optimizar tu tiempo y esfuerzo.

Reconocer y corregir estos errores comunes te permitirá realizar cálculos más precisos y eficientes en el futuro.

6. FAQ (Preguntas Frecuentes)

¿Cuál es la fórmula general para calcular el perímetro de un polígono?

La fórmula general para calcular el perímetro de un polígono es la suma de las longitudes de todos sus lados. Para un polígono regular, puedes usar fórmulas específicas basadas en el número de lados y la longitud de un lado. Por ejemplo, para un cuadrado, el perímetro es 4 veces la longitud de un lado, mientras que para un triángulo equilátero es 3 veces la longitud de un lado.

¿Cómo puedo calcular el perímetro de un polígono irregular sin medidas exactas?

Si no tienes medidas exactas, puedes estimar el perímetro utilizando una regla o cinta métrica. Otra opción es utilizar una cuadrícula para contar los lados y aproximar las longitudes. Sin embargo, ten en cuenta que esto solo proporcionará una estimación, no un cálculo preciso.

¿El perímetro se puede calcular para cualquier forma geométrica?

Sí, el perímetro se puede calcular para cualquier forma geométrica cerrada, siempre que puedas medir la longitud de cada lado. Sin embargo, para figuras más complejas, como círculos, se utilizan fórmulas específicas, como 2πr para el círculo, donde r es el radio.

¿Es necesario conocer el área para calcular el perímetro?

No, no es necesario conocer el área de un polígono para calcular su perímetro. El perímetro se basa únicamente en las longitudes de los lados. Sin embargo, en algunos contextos, conocer ambas medidas puede ser útil para resolver problemas más complejos.

¿Existen aplicaciones en la vida diaria donde se use el perímetro?

Sí, hay muchas aplicaciones en la vida diaria que requieren el cálculo del perímetro. Por ejemplo, al planificar una cerca para un jardín, al calcular la cantidad de pintura necesaria para cubrir las paredes de una habitación, o al diseñar un espacio en un plano arquitectónico. Estas son solo algunas de las situaciones en las que el perímetro es fundamental.

¿Cómo puedo practicar el cálculo del perímetro?

Una buena manera de practicar el cálculo del perímetro es realizar ejercicios que involucren diferentes tipos de polígonos. Puedes dibujar figuras en papel milimetrado y medir los lados, o buscar ejercicios en libros de matemáticas. También puedes crear problemas prácticos basados en situaciones de la vida real para aplicar lo que has aprendido.