¿Cuáles Son los Elementos que Forman una Fracción? Descubre su Estructura y Función

Las fracciones son una de las herramientas matemáticas más fundamentales que utilizamos en nuestra vida diaria, desde medir ingredientes en la cocina hasta calcular descuentos en las compras. Sin embargo, muchas personas no son completamente conscientes de la estructura que compone una fracción y de cómo se utilizan sus diferentes elementos. En este artículo, vamos a desglosar los componentes clave de una fracción, así como su función y relevancia en el mundo matemático. A medida que avancemos, descubrirás no solo qué son el numerador y el denominador, sino también cómo interactúan para expresar relaciones y proporciones. Prepárate para profundizar en el fascinante mundo de las fracciones y entender su papel esencial en las matemáticas y en la vida cotidiana.

1. ¿Qué es una Fracción?

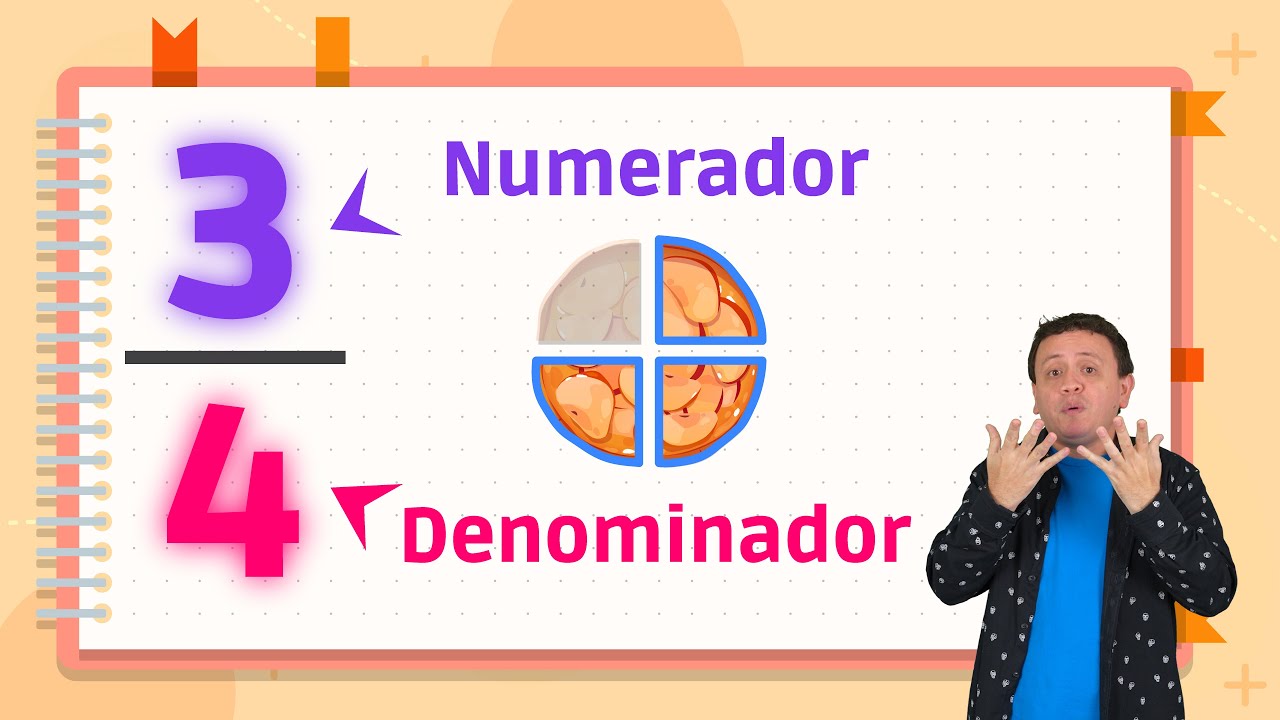
Una fracción es una representación numérica que expresa una parte de un todo. Se compone de dos números: el numerador y el denominador, que se separan por una línea horizontal o diagonal. Esta estructura permite entender cómo se divide un entero en partes iguales. Las fracciones pueden ser simples, como 1/2, o complejas, como 3/4 + 1/2. Para entender mejor este concepto, veamos cómo se construye una fracción y qué significa cada uno de sus elementos.

1.1. Definición de Numerador

El numerador es el número que se encuentra en la parte superior de la fracción. Representa cuántas partes del todo estamos considerando. Por ejemplo, en la fracción 3/4, el 3 es el numerador, lo que indica que estamos hablando de tres partes de un total de cuatro. Este elemento es fundamental porque nos dice la cantidad específica que estamos utilizando o analizando.

Un buen ejemplo de cómo funciona el numerador en la vida real es cuando compartimos una pizza. Si tenemos una pizza cortada en 8 rebanadas y decides comer 3, puedes representar esta situación con la fracción 3/8. Aquí, 3 es el numerador que indica cuántas rebanadas has tomado.

1.2. Definición de Denominador

El denominador es el número que se encuentra en la parte inferior de la fracción. Este número indica en cuántas partes iguales se ha dividido el todo. Siguiendo con el ejemplo anterior, en la fracción 3/4, el 4 es el denominador, lo que significa que el todo se ha dividido en cuatro partes iguales. Sin el denominador, no podríamos entender la proporción que representa el numerador.

Siguiendo con la pizza, si la pizza se cortó en 8 partes, el denominador sería 8. Así, la fracción que representa la cantidad de pizza que has comido es 3/8, donde 8 es el total de partes iguales en las que se dividió la pizza.

2. Tipos de Fracciones

Las fracciones no son todas iguales; existen varios tipos que se utilizan en diferentes contextos. Comprender las diferencias entre estos tipos es crucial para aplicar correctamente las fracciones en situaciones matemáticas. A continuación, exploraremos los tipos más comunes de fracciones y sus características.

2.1. Fracciones Propias

Las fracciones propias son aquellas en las que el numerador es menor que el denominador. Esto significa que la fracción representa una parte menor que el todo. Un ejemplo de fracción propia es 2/5. Aquí, el 2 es menor que el 5, lo que indica que estamos considerando dos de las cinco partes iguales.

Las fracciones propias son muy comunes en la vida diaria. Cuando medimos ingredientes para una receta, a menudo utilizamos fracciones propias, como 1/4 de taza de azúcar o 3/8 de cucharadita de sal. Estas fracciones nos ayudan a obtener las cantidades adecuadas sin exceder lo necesario.

2.2. Fracciones Impropias

Por otro lado, las fracciones impropias son aquellas en las que el numerador es igual o mayor que el denominador. Esto significa que la fracción representa un valor igual o mayor que uno. Por ejemplo, en la fracción 7/4, el 7 es mayor que el 4, lo que indica que tenemos más de un todo completo.

Las fracciones impropias se pueden encontrar en contextos donde necesitamos sumar partes que exceden el total. Por ejemplo, si tenemos 1 pizza y 3/4 de otra, podemos expresar esta cantidad como 7/4, indicando que tenemos más de una pizza completa.

2.3. Fracciones Mixtas

Las fracciones mixtas combinan un número entero con una fracción propia. Por ejemplo, 2 1/3 es una fracción mixta, donde el 2 representa el número entero y 1/3 es la fracción propia. Este tipo de fracción es útil cuando queremos expresar cantidades que son mayores que uno pero que también incluyen una parte fraccionaria.

Las fracciones mixtas son comunes en situaciones de la vida real, como cuando se mide la longitud o el volumen. Por ejemplo, si estás construyendo un mueble y necesitas 2 1/4 metros de madera, es más fácil y comprensible decir 2 1/4 en lugar de convertirlo a una fracción impropia.

3. Cómo Operar con Fracciones

Operar con fracciones puede parecer complicado al principio, pero una vez que entiendes los conceptos básicos, se vuelve más sencillo. Existen varias operaciones que puedes realizar con fracciones, incluyendo la suma, resta, multiplicación y división. Vamos a desglosar cada una de estas operaciones y cómo llevarlas a cabo.

3.1. Suma de Fracciones

Para sumar fracciones, es importante que tengan el mismo denominador. Si las fracciones tienen denominadores iguales, simplemente sumamos los numeradores y mantenemos el mismo denominador. Por ejemplo, para sumar 1/4 + 2/4, simplemente sumamos 1 + 2 = 3, manteniendo el denominador 4, lo que nos da 3/4.

Si las fracciones tienen denominadores diferentes, primero debemos encontrar un denominador común. Por ejemplo, para sumar 1/3 + 1/4, el denominador común sería 12. Convertimos las fracciones a 4/12 y 3/12, respectivamente, y luego sumamos: 4/12 + 3/12 = 7/12.

3.2. Resta de Fracciones

La resta de fracciones sigue el mismo principio que la suma. Si las fracciones tienen el mismo denominador, restamos los numeradores y mantenemos el denominador. Por ejemplo, 3/5 – 1/5 = 2/5.

Si los denominadores son diferentes, encontramos un denominador común. Por ejemplo, para restar 2/3 – 1/6, el denominador común sería 6. Convertimos 2/3 a 4/6 y luego realizamos la resta: 4/6 – 1/6 = 3/6, que se simplifica a 1/2.

3.3. Multiplicación de Fracciones

Multiplicar fracciones es bastante sencillo. Simplemente multiplicamos los numeradores entre sí y los denominadores entre sí. Por ejemplo, para multiplicar 2/3 * 3/4, multiplicamos 2 * 3 = 6 y 3 * 4 = 12, resultando en 6/12, que se simplifica a 1/2.

Es importante recordar que no necesitamos un denominador común para multiplicar fracciones, lo que hace que esta operación sea más directa que la suma o la resta.

4. La Importancia de las Fracciones en la Vida Cotidiana

Las fracciones juegan un papel crucial en nuestras actividades diarias, a menudo sin que nos demos cuenta. Desde cocinar hasta manejar finanzas, el uso de fracciones es omnipresente. Aquí te mostramos algunas de las formas en que las fracciones son esenciales en la vida cotidiana.

4.1. Cocina y Repostería

Una de las áreas donde las fracciones son más útiles es en la cocina. Al seguir recetas, a menudo necesitamos medir ingredientes en fracciones. Por ejemplo, si una receta requiere 3/4 de taza de harina, sabemos que necesitamos un poco menos que una taza completa. Aquí, las fracciones nos permiten ajustar las cantidades según nuestras necesidades, especialmente si estamos cocinando para más o menos personas.

Además, cuando duplicamos o reducimos recetas, las fracciones nos ayudan a calcular rápidamente las nuevas cantidades. Si una receta que sirve a cuatro personas se duplica, y originalmente pide 1/2 taza de azúcar, entonces necesitamos 1 taza, que es el doble. Las fracciones hacen que estas conversiones sean fáciles de realizar.

4.2. Finanzas Personales

En el ámbito financiero, las fracciones son fundamentales para entender conceptos como tasas de interés, descuentos y proporciones. Por ejemplo, si tienes un descuento del 25% en un artículo, esto se traduce en la fracción 1/4, lo que significa que pagarás 3/4 del precio original. Saber cómo trabajar con fracciones te permite tomar decisiones más informadas sobre tus compras y ahorros.

Asimismo, al calcular intereses en cuentas de ahorro o préstamos, las fracciones son utilizadas para determinar cuánto dinero ganarás o deberás pagar. Por ejemplo, si un préstamo tiene una tasa de interés del 5%, esto se puede expresar como la fracción 5/100, lo que facilita entender el costo del préstamo a lo largo del tiempo.

5. Preguntas Frecuentes sobre Fracciones

5.1. ¿Qué es una fracción equivalente?

Las fracciones equivalentes son aquellas que representan la misma cantidad o proporción, aunque tengan diferentes numeradores y denominadores. Por ejemplo, 1/2 y 2/4 son fracciones equivalentes porque ambas representan la misma parte del todo. Para encontrar fracciones equivalentes, puedes multiplicar o dividir el numerador y el denominador por el mismo número. Esto es útil cuando simplificamos fracciones o al realizar operaciones matemáticas.

5.2. ¿Cómo se simplifican las fracciones?

Para simplificar una fracción, debes encontrar el máximo común divisor (MCD) del numerador y el denominador y dividir ambos por ese número. Por ejemplo, para simplificar la fracción 8/12, el MCD de 8 y 12 es 4. Al dividir ambos por 4, obtenemos 2/3, que es la forma simplificada de la fracción. La simplificación es importante porque facilita la comprensión y el uso de las fracciones en cálculos posteriores.

5.3. ¿Cuándo se utilizan fracciones en la educación?

Las fracciones se introducen en la educación básica, generalmente en la escuela primaria, y son un componente clave del currículo de matemáticas. Se enseñan para ayudar a los estudiantes a comprender conceptos de división y proporciones. A medida que los estudiantes avanzan, aprenderán a operar con fracciones y a aplicar estos conocimientos en problemas más complejos, como el álgebra y la geometría.

5.4. ¿Las fracciones pueden ser negativas?

Sí, las fracciones pueden ser negativas. Una fracción negativa se representa con un signo negativo delante del numerador o del denominador. Por ejemplo, -3/4 y 3/-4 son ambas fracciones negativas que representan la misma cantidad. Las fracciones negativas son útiles en situaciones donde se representan pérdidas o deudas, y se utilizan de la misma manera que las fracciones positivas en las operaciones matemáticas.

5.5. ¿Cómo se convierten fracciones en decimales?

Para convertir una fracción en un número decimal, simplemente divide el numerador entre el denominador. Por ejemplo, para convertir 3/4 a decimal, dividirías 3 entre 4, lo que resulta en 0.75. Esta conversión es útil en diversas aplicaciones, como en finanzas o en situaciones donde se prefiere un formato decimal en lugar de fraccionario.

5.6. ¿Qué son las fracciones decimales?

Las fracciones decimales son aquellas cuyo denominador es una potencia de 10, como 10, 100 o 1000. Por ejemplo, 0.75 es una fracción decimal que puede expresarse como 75/100. Las fracciones decimales son comunes en matemáticas y se utilizan frecuentemente en cálculos financieros y en situaciones donde se requiere precisión.

5.7. ¿Cómo se relacionan las fracciones con los porcentajes?

Las fracciones y los porcentajes están estrechamente relacionados, ya que ambos representan partes de un todo. Un porcentaje es una fracción con un denominador de 100. Por ejemplo, 25% se puede expresar como 25/100, que también se simplifica a 1/4. Comprender esta relación es esencial para resolver problemas que involucran descuentos, aumentos y proporciones en situaciones cotidianas.