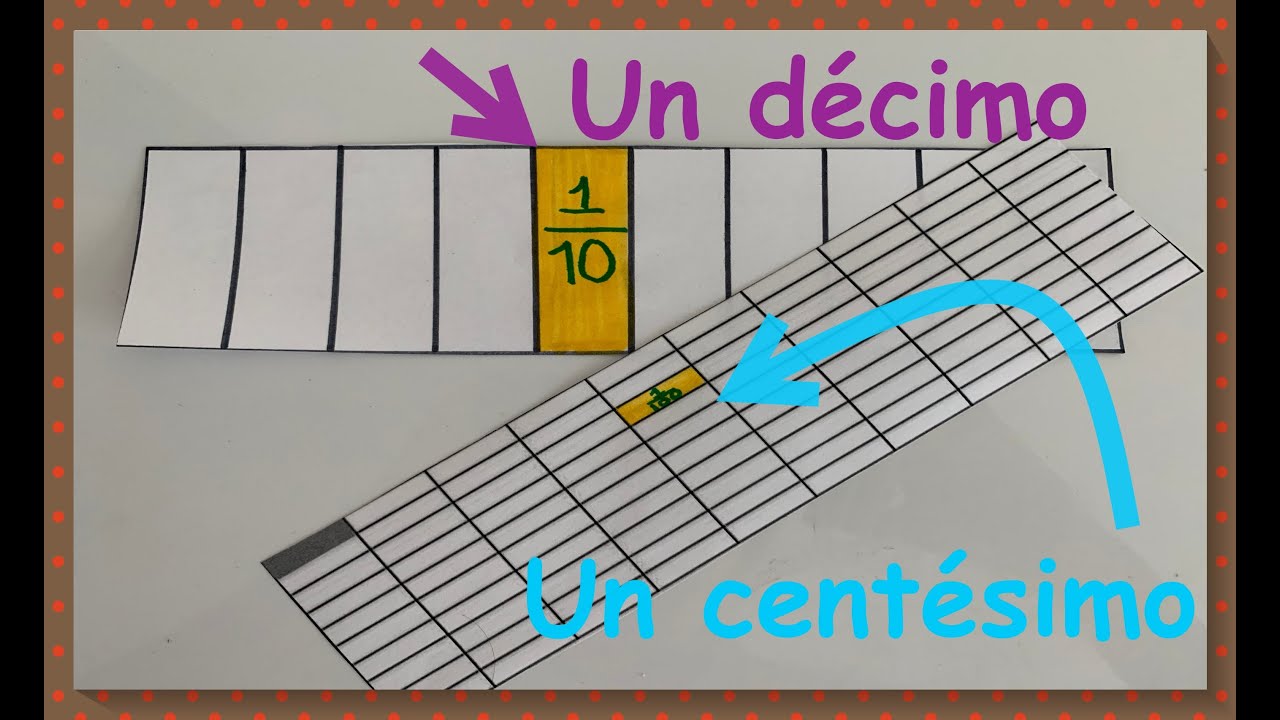
¿Cuántos centésimos equivalen a un décimo? Descubre la respuesta y su explicación clara

En el mundo de las matemáticas y las finanzas, entender las relaciones entre diferentes unidades es fundamental. Una de las preguntas más comunes que surge es: ¿cuántos centésimos equivalen a un décimo? Este concepto, aunque simple, es esencial para manejar operaciones básicas y también para comprender temas más complejos como porcentajes y proporciones. En este artículo, vamos a desglosar este tema de manera clara y concisa, ofreciendo una explicación que no solo responde a la pregunta inicial, sino que también te ayudará a ver la conexión entre décimos y centésimos de una forma más amplia.

A lo largo de este artículo, exploraremos las definiciones de décimos y centésimos, cómo se relacionan entre sí y su importancia en diferentes contextos. También te proporcionaremos ejemplos prácticos y consejos útiles para que puedas aplicar este conocimiento en tu vida diaria. Si alguna vez te has preguntado sobre la equivalencia entre estas dos unidades, sigue leyendo para descubrirlo de manera sencilla y efectiva.

¿Qué son los décimos?

Los décimos son una fracción que representa una parte de diez. En términos matemáticos, un décimo se escribe como 1/10. Esto significa que si tienes un todo dividido en diez partes iguales, cada parte se considera un décimo. Para entenderlo mejor, imaginemos un pastel que se ha cortado en diez porciones iguales. Cada porción representa un décimo del pastel.

Ejemplo de décimos en la vida cotidiana

Imagina que estás en una tienda y decides comprar un producto que cuesta 10 euros. Si decides comprar solo un décimo del producto, estarías pagando 1 euro, ya que 10 euros dividido por 10 es igual a 1 euro. Esta relación es fundamental en el manejo de dinero y en la comprensión de precios y descuentos.

La representación decimal de los décimos

Los décimos también pueden expresarse en forma decimal. Un décimo se representa como 0.1. Esto es útil porque muchas operaciones matemáticas se realizan con números decimales, y entender cómo convertir entre fracciones y decimales es crucial. Así que cuando veas 0.1, recuerda que se refiere a un décimo.

¿Qué son los centésimos?

Por otro lado, los centésimos representan una fracción que se obtiene al dividir algo en cien partes iguales. Matemáticamente, un centésimo se expresa como 1/100. Siguiendo con el ejemplo del pastel, si lo cortas en cien porciones, cada porción sería un centésimo del pastel.

Ejemplo de centésimos en la vida cotidiana

Supongamos que compras un producto que cuesta 100 euros. Si decides comprar un centésimo de este producto, pagarías 1 euro, ya que 100 euros dividido por 100 es igual a 1 euro. Este tipo de cálculo es común en situaciones donde se manejan porcentajes, como en descuentos o impuestos.

La representación decimal de los centésimos

Al igual que los décimos, los centésimos también tienen su representación decimal. Un centésimo se expresa como 0.01. Esta forma decimal es esencial para realizar cálculos en diversas situaciones, especialmente en finanzas y estadísticas.

Relación entre décimos y centésimos

Ahora que hemos definido qué son los décimos y los centésimos, es el momento de responder a la pregunta clave: ¿cuántos centésimos equivalen a un décimo? La respuesta es bastante sencilla: un décimo equivale a diez centésimos. Esto se puede entender mejor al observar sus representaciones decimales: 0.1 (décimo) es igual a 0.10 (diez centésimos).

Demostración matemática de la equivalencia

Para demostrarlo, podemos realizar la siguiente operación matemática: si un décimo es 1/10, para convertirlo a centésimos, multiplicamos por 10. Así que:

• 1 décimo = 1/10
• Multiplicamos por 10 para convertir a centésimos: (1/10) * (10/10) = 10/100
• Esto nos da 10 centésimos.

Así que, efectivamente, un décimo es igual a diez centésimos. Esta relación es fundamental no solo en matemáticas básicas, sino también en situaciones cotidianas donde se manejan porcentajes y fracciones.

Aplicaciones prácticas de la equivalencia

Entender cuántos centésimos equivalen a un décimo es útil en diversas situaciones. Por ejemplo:

• Calcular descuentos: Si un producto tiene un 10% de descuento, esto significa que estás ahorrando 10 centésimos de cada euro que gastas.
• Distribución de recursos: En un grupo de diez personas, si decides repartir 100 euros, cada persona recibiría 10 centésimos de cada euro.

Estas aplicaciones demuestran cómo este conocimiento puede ser útil en la vida diaria y en la toma de decisiones financieras.

La importancia de entender las fracciones y sus equivalencias

Comprender las fracciones y sus equivalencias es esencial en muchos aspectos de la vida. Desde el ámbito académico hasta el financiero, las fracciones son herramientas fundamentales que nos permiten expresar cantidades de manera precisa. Además, tener una buena base en fracciones ayuda a desarrollar habilidades matemáticas más avanzadas.

Fracciones en la educación matemática

En el contexto educativo, las fracciones son uno de los temas clave que los estudiantes deben dominar. Desde la primaria, los alumnos aprenden a trabajar con fracciones, lo que sienta las bases para conceptos más complejos como el cálculo de porcentajes y proporciones. La habilidad para convertir entre fracciones, decimales y porcentajes es crucial para el éxito en matemáticas y en la vida diaria.

Fracciones en la vida cotidiana

Además de su importancia educativa, las fracciones son omnipresentes en la vida cotidiana. Desde recetas de cocina que requieren fracciones de ingredientes hasta la gestión de presupuestos personales, la capacidad de entender y trabajar con fracciones es vital. Por ejemplo, si una receta pide 2/3 de taza de azúcar, saber cómo medir y calcular esta cantidad es esencial para obtener el resultado deseado.

FAQ (Preguntas Frecuentes)

1. ¿Por qué es importante saber cuántos centésimos equivalen a un décimo?

Conocer la equivalencia entre décimos y centésimos es esencial para realizar cálculos financieros, manejar porcentajes y tomar decisiones informadas en situaciones cotidianas. Por ejemplo, en promociones y descuentos, saber que un décimo equivale a diez centésimos te ayuda a entender cuánto estás ahorrando realmente.

2. ¿Cómo puedo convertir un décimo a centésimos fácilmente?

Para convertir un décimo a centésimos, simplemente multiplica por 10. Por ejemplo, si tienes 0.1 (un décimo), al multiplicarlo por 10 obtienes 1.0, que representa diez centésimos. Esta regla te permitirá hacer conversiones rápidas y efectivas.

3. ¿Se pueden aplicar décimos y centésimos en situaciones de la vida diaria?

Definitivamente. Tanto los décimos como los centésimos se utilizan en situaciones cotidianas como calcular precios, descuentos y proporciones en recetas. Comprender estas fracciones te ayuda a manejar mejor tus finanzas y a tomar decisiones informadas.

4. ¿Qué otras fracciones son útiles en matemáticas?

Además de décimos y centésimos, hay muchas otras fracciones útiles como los quintos (1/5), cuartos (1/4) y tercios (1/3). Cada una de estas fracciones tiene aplicaciones en diferentes contextos, como la cocina, la construcción y las finanzas. Comprenderlas te dará una ventaja en diversas situaciones.

5. ¿Cómo puedo practicar la conversión entre fracciones y decimales?

Una excelente manera de practicar es utilizar ejercicios en línea, libros de matemáticas o aplicaciones educativas. Puedes empezar con fracciones simples y luego avanzar a problemas más complejos. Además, hacer ejercicios prácticos en situaciones reales, como calcular descuentos en compras, puede ser muy útil.

6. ¿Los centésimos son solo útiles en matemáticas o tienen aplicaciones en otras áreas?

Los centésimos tienen aplicaciones en muchas áreas, incluyendo finanzas, estadísticas y ciencias. En finanzas, se utilizan para calcular tasas de interés y rendimientos, mientras que en estadísticas, son fundamentales para expresar datos en porcentajes. Por lo tanto, son relevantes en diversas disciplinas.

7. ¿Puedo utilizar calculadoras para trabajar con décimos y centésimos?

Por supuesto, las calculadoras son herramientas muy útiles para trabajar con décimos y centésimos. Puedes ingresar las fracciones y obtener resultados rápidos. Sin embargo, es importante entender los conceptos básicos para saber cómo interpretar los resultados y aplicarlos correctamente en situaciones del mundo real.