Elementos Básicos de la Geometría Plana: Guía Completa para Entender sus Fundamentos
La geometría plana es una de las ramas más fundamentales de las matemáticas, y su comprensión es esencial para diversas disciplinas, desde la arquitectura hasta la ingeniería y el arte. Si alguna vez te has preguntado cómo se relacionan las figuras en un plano, o cómo se calculan áreas y perímetros, este artículo es para ti. Aquí desglosaremos los elementos básicos de la geometría plana, explicando conceptos clave como puntos, líneas, ángulos y figuras geométricas, así como sus propiedades y fórmulas. Además, abordaremos aplicaciones prácticas y ejemplos que te ayudarán a entender mejor estos fundamentos. Prepárate para sumergirte en el fascinante mundo de la geometría plana y descubrir cómo estos elementos se entrelazan para formar la base de muchas estructuras que vemos a nuestro alrededor.
Puntos, Líneas y Segmentos
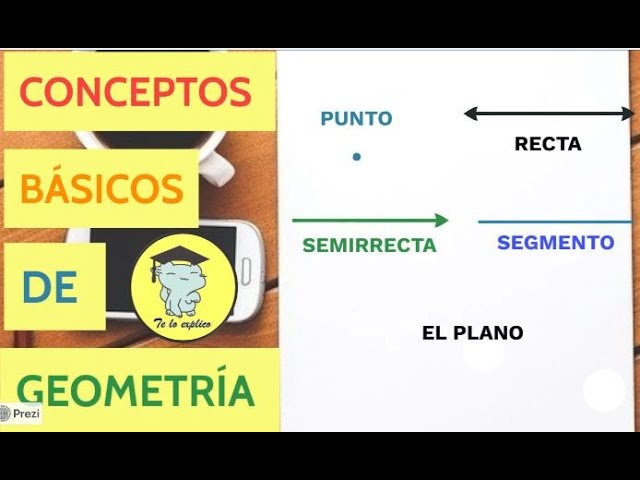
Comencemos con los conceptos más básicos de la geometría plana: los puntos y las líneas. Un punto es una entidad que no tiene dimensiones; simplemente indica una ubicación en el espacio. Aunque no podemos visualizarlo como un objeto físico, podemos representarlo gráficamente con un pequeño círculo. Por otro lado, una línea es una sucesión infinita de puntos que se extiende en dos direcciones, y se puede representar en un plano con una línea recta. Las líneas pueden ser rectas, curvas o quebradas.
Segmentos de Línea
Un segmento de línea es una parte de una línea que tiene dos extremos. Este concepto es fundamental en la geometría, ya que nos permite medir distancias. La longitud de un segmento de línea se puede calcular utilizando la fórmula de la distancia entre dos puntos en un plano cartesiano. Si tenemos dos puntos A(x1, y1) y B(x2, y2), la distancia se calcula así:
Distancia = √[(x2 – x1)² + (y2 – y1)²]
Por ejemplo, si A(1, 2) y B(4, 6), la distancia sería:
Distancia = √[(4 – 1)² + (6 – 2)²] = √[9 + 16] = √25 = 5
Intersecciones y Paralelismo
En geometría, las líneas pueden intersectarse o ser paralelas. Cuando dos líneas se cruzan, forman ángulos en el punto de intersección. Por otro lado, si dos líneas son paralelas, nunca se cruzan, sin importar cuánto se extiendan. Esto es crucial en el diseño arquitectónico, donde se deben considerar las distancias y la alineación de las estructuras. Comprender cómo funcionan estas interacciones es esencial para resolver problemas geométricos más complejos.
Ángulos: Medición y Clasificación
Los ángulos son figuras formadas por dos segmentos de línea que se encuentran en un punto común, conocido como vértice. La medida de un ángulo se expresa en grados y se clasifica en diferentes tipos: agudo, recto, obtuso y llano. Un ángulo agudo mide menos de 90 grados, un ángulo recto mide exactamente 90 grados, un ángulo obtuso mide más de 90 grados pero menos de 180 grados, y un ángulo llano mide exactamente 180 grados.
Propiedades de los Ángulos
Una de las propiedades más importantes de los ángulos es que la suma de los ángulos en un triángulo siempre es igual a 180 grados. Esta propiedad es fundamental para resolver problemas relacionados con triángulos. Además, los ángulos adyacentes, que comparten un lado y un vértice, también son relevantes. Por ejemplo, si tienes un ángulo de 40 grados, su ángulo complementario será de 50 grados, ya que 40 + 50 = 90.
Ángulos Complementarios y Suplementarios
Los ángulos complementarios son aquellos que suman 90 grados, mientras que los ángulos suplementarios son aquellos cuya suma es 180 grados. Conocer estas definiciones es crucial para resolver problemas en geometría, ya que te permitirá deducir medidas de ángulos que no se conocen. Por ejemplo, si tienes un ángulo de 70 grados, su ángulo complementario será de 20 grados (90 – 70), y su ángulo suplementario será de 110 grados (180 – 70).
Figuras Geométricas Planas
Las figuras geométricas planas son formas que se encuentran en un plano y se clasifican en dos categorías principales: polígonos y figuras no poligonales. Los polígonos son formas cerradas que están formadas por segmentos de línea, mientras que las figuras no poligonales incluyen círculos y elipses. Cada figura tiene sus propias propiedades y fórmulas para calcular área y perímetro.
Polígonos: Clasificación y Propiedades
Los polígonos se pueden clasificar según el número de lados. Un triángulo tiene tres lados, un cuadrado tiene cuatro, un pentágono tiene cinco y así sucesivamente. La suma de los ángulos interiores de un polígono se puede calcular con la fórmula (n – 2) * 180, donde n es el número de lados. Por ejemplo, en un cuadrado, n = 4, por lo que la suma de los ángulos es (4 – 2) * 180 = 360 grados.
Círculos y su Importancia
El círculo es una figura no poligonal que tiene una serie de propiedades únicas. La distancia desde el centro del círculo hasta cualquier punto en su borde se llama radio. El diámetro es el doble del radio y es la distancia a través del círculo que pasa por el centro. La fórmula para calcular el área de un círculo es A = π * r², donde r es el radio, y el perímetro (circunferencia) se calcula como C = 2 * π * r. Estas fórmulas son esenciales en diversas aplicaciones, desde la ingeniería hasta el diseño gráfico.
Área y Perímetro: Cálculos Fundamentales
Entender cómo calcular el área y el perímetro de diferentes figuras geométricas es vital en la geometría plana. El área se refiere a la medida de la superficie de una figura, mientras que el perímetro es la longitud del contorno de la figura. Cada figura tiene su propia fórmula para calcular estas medidas, lo que hace que sea esencial conocerlas.
Cálculo del Área
Por ejemplo, para calcular el área de un cuadrado, utilizamos la fórmula A = lado². Si un cuadrado tiene lados de 5 unidades, su área será 5² = 25 unidades cuadradas. Para un rectángulo, la fórmula es A = base * altura. Si un rectángulo tiene una base de 4 unidades y una altura de 6 unidades, su área será 4 * 6 = 24 unidades cuadradas. Estos cálculos son fundamentales para una variedad de aplicaciones prácticas, desde la construcción hasta la planificación de jardines.
Cálculo del Perímetro
El cálculo del perímetro también es esencial. Para un cuadrado, el perímetro se calcula como P = 4 * lado. En el caso de un rectángulo, se usa la fórmula P = 2 * (base + altura). Por ejemplo, si un rectángulo tiene una base de 4 unidades y una altura de 6 unidades, su perímetro será 2 * (4 + 6) = 20 unidades. Estos conceptos son importantes para entender la forma en que se relacionan las dimensiones de las figuras y cómo se aplican en situaciones del mundo real.
Transformaciones Geométricas
Las transformaciones geométricas son operaciones que permiten cambiar la posición, tamaño o forma de una figura en el plano. Las principales transformaciones incluyen la traslación, rotación y reflexión. Estas transformaciones son fundamentales en la geometría y tienen aplicaciones en diversas áreas, como el diseño gráfico y la programación.
Traslación
La traslación implica mover una figura de un lugar a otro sin cambiar su forma o tamaño. Por ejemplo, si trasladas un triángulo 3 unidades a la derecha y 2 unidades hacia arriba, la figura seguirá siendo un triángulo, pero en una nueva posición. Este concepto es esencial en el estudio de coordenadas y en la comprensión de cómo se mueven las figuras en un plano.
Rotación y Reflexión
La rotación consiste en girar una figura alrededor de un punto fijo, conocido como el centro de rotación. Por ejemplo, si giras un cuadrado 90 grados alrededor de su centro, obtendrás una nueva posición de la misma figura. Por otro lado, la reflexión implica voltear una figura a través de una línea, creando una imagen especular. Estas transformaciones no solo son teóricas; tienen aplicaciones prácticas en el arte y la ingeniería, donde la manipulación de formas es fundamental.
Aplicaciones Prácticas de la Geometría Plana
La geometría plana tiene numerosas aplicaciones en la vida diaria y en diversas profesiones. Desde la arquitectura hasta la ingeniería, el diseño gráfico y la fabricación, los conceptos geométricos son fundamentales para la creación de estructuras y objetos. Por ejemplo, al diseñar un edificio, los arquitectos utilizan principios de geometría para garantizar que las proporciones y medidas sean correctas. Además, en la fabricación de productos, la geometría se aplica para asegurar que las piezas encajen correctamente.
Geometría en la Vida Diaria
En nuestra vida diaria, la geometría plana está presente en objetos cotidianos. Desde las mesas y sillas que usamos hasta los diseños de los edificios y las calles, todos estos elementos se basan en principios geométricos. La planificación de un jardín, la creación de un mural o incluso la disposición de los muebles en una habitación son ejemplos de cómo la geometría influye en nuestras decisiones diarias.
Educación y Geometría
La educación en geometría es esencial para desarrollar habilidades de pensamiento crítico y resolución de problemas. A través del aprendizaje de la geometría, los estudiantes no solo adquieren conocimientos teóricos, sino que también aprenden a aplicar estos conceptos en situaciones del mundo real. Esto no solo les prepara para futuras carreras en campos técnicos, sino que también les ayuda a desarrollar habilidades que son útiles en la vida cotidiana.
Preguntas Frecuentes (FAQ)
¿Qué es la geometría plana?
La geometría plana es una rama de las matemáticas que estudia las figuras y propiedades en un plano bidimensional. Se centra en conceptos como puntos, líneas, ángulos y diversas figuras geométricas, así como sus interacciones y propiedades. Es fundamental para entender cómo se relacionan las formas y cómo se aplican en situaciones del mundo real.
¿Cuáles son los tipos de ángulos y sus características?
Los ángulos se clasifican en agudos (menos de 90 grados), rectos (exactamente 90 grados), obtusos (más de 90 grados pero menos de 180 grados) y llanos (exactamente 180 grados). Cada tipo de ángulo tiene propiedades específicas que son importantes en la resolución de problemas geométricos y en la comprensión de las relaciones entre diferentes figuras.
¿Cómo se calcula el área de un círculo?
El área de un círculo se calcula utilizando la fórmula A = π * r², donde r es el radio del círculo. Esto significa que debes elevar al cuadrado la longitud del radio y luego multiplicar por π (aproximadamente 3.14). Por ejemplo, si el radio es 3 unidades, el área sería A = π * 3² = π * 9, que es aproximadamente 28.27 unidades cuadradas.
¿Qué son los polígonos y cómo se clasifican?
Los polígonos son figuras cerradas formadas por segmentos de línea. Se clasifican según el número de lados: triángulos (3 lados), cuadriláteros (4 lados), pentágonos (5 lados), hexágonos (6 lados), etc. Cada tipo de polígono tiene propiedades y fórmulas específicas para calcular su área y perímetro, lo que los hace importantes en la geometría.
¿Cuál es la diferencia entre área y perímetro?
El área se refiere a la medida de la superficie de una figura, mientras que el perímetro es la longitud total del contorno de la figura. Por ejemplo, en un cuadrado, el área se calcula como lado² y el perímetro como 4 * lado. Ambos conceptos son fundamentales en la geometría y se aplican en diversas situaciones prácticas.
¿Qué son las transformaciones geométricas?
Las transformaciones geométricas son operaciones que cambian la posición, tamaño o forma de una figura en el plano. Las principales transformaciones incluyen la traslación (movimiento), rotación (giro) y reflexión (simetría). Estas transformaciones son esenciales en la geometría y tienen aplicaciones en diseño gráfico, ingeniería y más.
¿Por qué es importante estudiar geometría plana?
Estudiar geometría plana es importante porque proporciona habilidades de pensamiento crítico y resolución de problemas. Además, los conceptos geométricos son fundamentales en diversas profesiones, como la arquitectura y la ingeniería. La geometría también está presente en la vida diaria, lo que la convierte en una disciplina esencial para entender el mundo que nos rodea.