Fórmulas de Perímetros y Áreas de Polígonos: Guía Completa para Estudiantes
¿Alguna vez te has preguntado cómo calcular el perímetro o el área de un polígono? Estas son habilidades fundamentales en matemáticas que no solo son esenciales para tus estudios, sino que también tienen aplicaciones prácticas en la vida cotidiana. En esta guía completa, exploraremos las fórmulas de perímetros y áreas de varios tipos de polígonos, desde los más simples hasta los más complejos. Aprenderás no solo las fórmulas, sino también cómo aplicarlas con ejemplos claros y prácticos. Al final de este artículo, estarás preparado para abordar cualquier problema relacionado con polígonos que se te presente. ¡Comencemos!
1. ¿Qué es un Polígono?
Antes de profundizar en las fórmulas, es importante entender qué es un polígono. Un polígono es una figura geométrica plana que se compone de tres o más lados rectos. Los polígonos pueden clasificarse en varias categorías, dependiendo de la cantidad de lados y de sus características. Vamos a desglosar esto un poco más.
1.1 Clasificación de Polígonos
Los polígonos se pueden clasificar de varias maneras:
- Por el número de lados: Triángulos (3 lados), cuadriláteros (4 lados), pentágonos (5 lados), hexágonos (6 lados), y así sucesivamente.
- Por la regularidad: Un polígono regular tiene todos sus lados y ángulos iguales, mientras que un polígono irregular no cumple con esta condición.
1.2 Ejemplos de Polígonos
Algunos ejemplos de polígonos son:
- Triángulo equilátero
- Cuadrado
- Pentágono regular
- Hexágono irregular
Entender la clasificación de los polígonos te ayudará a aplicar las fórmulas correctas para calcular perímetros y áreas en las secciones siguientes.
2. Fórmulas de Perímetros de Polígonos
El perímetro de un polígono es la suma de la longitud de todos sus lados. Calcular el perímetro es esencial en muchas situaciones, como al diseñar espacios o al medir materiales. A continuación, te mostramos cómo calcular el perímetro de diferentes tipos de polígonos.
2.1 Perímetro de Triángulos
Para calcular el perímetro de un triángulo, simplemente suma las longitudes de sus tres lados:
Fórmula: P = a + b + c
Donde «a», «b» y «c» son las longitudes de los lados del triángulo. Por ejemplo, si un triángulo tiene lados de 3 cm, 4 cm y 5 cm, su perímetro sería:
P = 3 + 4 + 5 = 12 cm
2.2 Perímetro de Cuadriláteros
Para un cuadrilátero, el perímetro se calcula sumando las longitudes de sus cuatro lados:
Fórmula: P = a + b + c + d
Si tenemos un cuadrado, todos los lados son iguales, por lo que se puede simplificar a:
P = 4 * l
Donde «l» es la longitud de un lado. Por ejemplo, si un cuadrado tiene lados de 5 cm, su perímetro sería:
P = 4 * 5 = 20 cm
2.3 Perímetro de Polígonos Regulares
Para calcular el perímetro de un polígono regular, que tiene todos sus lados y ángulos iguales, utilizamos la siguiente fórmula:
Fórmula: P = n * l
Donde «n» es el número de lados y «l» es la longitud de un lado. Por ejemplo, para un pentágono regular con lados de 6 cm:
P = 5 * 6 = 30 cm
3. Fórmulas de Áreas de Polígonos
El área de un polígono es la medida de la superficie encerrada dentro de sus lados. Calcular el área es crucial en campos como la arquitectura y la planificación urbana. Vamos a revisar cómo se calcula el área de diferentes tipos de polígonos.
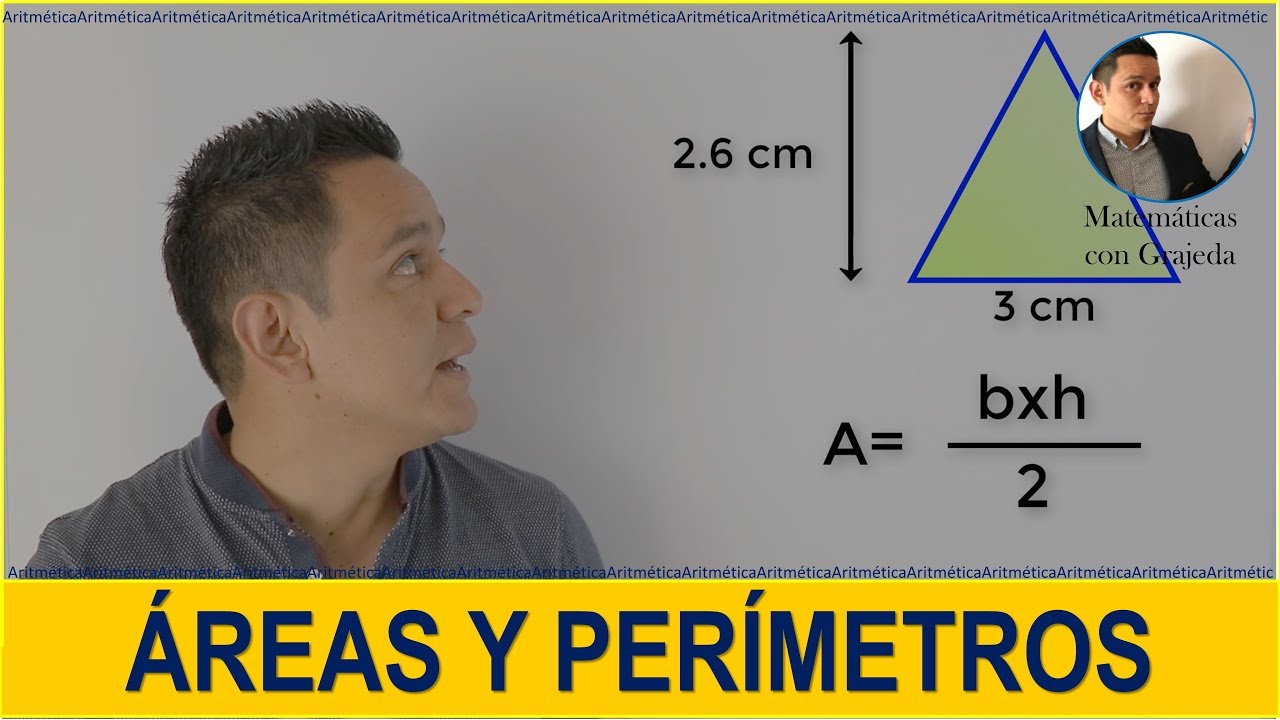
3.1 Área de Triángulos
El área de un triángulo se puede calcular usando la siguiente fórmula:
Fórmula: A = (b * h) / 2
Donde «b» es la base y «h» es la altura del triángulo. Por ejemplo, si un triángulo tiene una base de 4 cm y una altura de 3 cm:
A = (4 * 3) / 2 = 6 cm²
3.2 Área de Cuadriláteros
Para un cuadrado, el área se calcula como:
Fórmula: A = l²
Donde «l» es la longitud de un lado. Si el lado mide 5 cm:
A = 5² = 25 cm²
Para un rectángulo, la fórmula es:
Fórmula: A = b * h
Donde «b» es la base y «h» es la altura. Si la base mide 6 cm y la altura 4 cm:
A = 6 * 4 = 24 cm²
3.3 Área de Polígonos Regulares
El área de un polígono regular se puede calcular con la siguiente fórmula:
Fórmula: A = (Perímetro * Apotema) / 2
El apotema es la distancia desde el centro del polígono hasta el medio de un lado. Por ejemplo, para un hexágono regular con un perímetro de 24 cm y un apotema de 5 cm:
A = (24 * 5) / 2 = 60 cm²
4. Aplicaciones Prácticas de las Fórmulas de Perímetros y Áreas
Las fórmulas de perímetros y áreas no son solo conceptos teóricos; tienen numerosas aplicaciones prácticas. Aquí te mostramos algunas de ellas.
4.1 Diseño de Espacios
Al diseñar un jardín o una habitación, es esencial conocer el área para determinar cuántos materiales se necesitarán, como césped o pintura. Por ejemplo, si quieres colocar césped en un jardín rectangular de 10 m de largo por 5 m de ancho, calcular el área te dirá cuántos metros cuadrados de césped comprar.
4.2 Construcción y Arquitectura
Los arquitectos utilizan estas fórmulas para diseñar edificios y estructuras. Conocer el área y el perímetro de las habitaciones ayuda a optimizar el uso del espacio y a cumplir con los códigos de construcción. Por ejemplo, si un arquitecto planea una sala de estar de 20 m², debe asegurarse de que el diseño sea funcional y estéticamente agradable.
4.3 Jardinería y Agricultura
En la agricultura, calcular el área de los cultivos es vital para estimar la producción y el uso de recursos. Un agricultor que cultiva en un terreno rectangular de 100 m de largo y 50 m de ancho puede calcular su área cultivable para planificar la siembra.
5. Consejos para Resolver Problemas de Perímetros y Áreas
Resolver problemas relacionados con perímetros y áreas puede parecer complicado, pero con algunos consejos, se vuelve mucho más sencillo.
5.1 Dibuja el Polígono
Una de las mejores maneras de abordar un problema es dibujar el polígono. Esto te ayudará a visualizar los lados y las dimensiones, lo que facilita el cálculo del perímetro y el área.
5.2 Utiliza Unidades Consistentes
Asegúrate de que todas las medidas estén en la misma unidad antes de hacer cálculos. Si tienes un lado en centímetros y otro en metros, conviértelos a la misma unidad para evitar errores.
5.3 Practica con Ejercicios
La práctica hace al maestro. Realiza ejercicios de diferentes tipos de polígonos para familiarizarte con las fórmulas. Cuanto más practiques, más fácil te será recordar y aplicar las fórmulas en situaciones reales.
6. Preguntas Frecuentes (FAQ)
¿Cuál es la diferencia entre perímetro y área?
El perímetro es la longitud total de todos los lados de un polígono, mientras que el área es la medida de la superficie encerrada dentro de esos lados. En términos simples, el perímetro mide el contorno, y el área mide el espacio interior.
¿Cómo se calcula el área de un triángulo si no conozco la altura?
Si no conoces la altura, pero conoces las longitudes de los lados, puedes utilizar la fórmula de Herón. Primero, calcula el semiperímetro (s = (a + b + c) / 2), y luego usa A = √(s(s-a)(s-b)(s-c)) para encontrar el área.
¿Puedo usar las fórmulas de área y perímetro en polígonos irregulares?
Para los polígonos irregulares, puedes dividir el polígono en formas más simples (triángulos, rectángulos) y calcular el área de cada una, sumando luego los resultados. El perímetro se calcula sumando la longitud de todos los lados.
¿Qué pasa si un polígono tiene lados de diferentes longitudes?
Para calcular el perímetro, simplemente suma la longitud de todos los lados, independientemente de si son iguales o no. Para el área, necesitarás una fórmula específica dependiendo de la forma del polígono.
¿Existen calculadoras para perímetros y áreas de polígonos?
Sí, hay muchas calculadoras en línea que te permiten ingresar las dimensiones de un polígono y te devuelven automáticamente el perímetro y el área. Estas herramientas son muy útiles para verificar tus cálculos.
¿Cómo se aplican estas fórmulas en la vida real?
Las fórmulas de perímetros y áreas se utilizan en diversas áreas, como la arquitectura, la jardinería, la planificación urbana y la agricultura. Conocer estas medidas es esencial para el diseño eficiente y el uso adecuado de espacios.