¿Qué es la división y sus partes? Explicación clara y sencilla
La división es una de las operaciones matemáticas más fundamentales y esenciales en nuestra vida diaria. Desde repartir una pizza entre amigos hasta calcular cuánto tiempo tomará un proyecto, la división está presente en diversas situaciones cotidianas. Pero, ¿qué es exactamente la división y cuáles son sus partes? En este artículo, exploraremos a fondo este concepto matemático, desglosando sus componentes y ofreciendo ejemplos prácticos que te ayudarán a comprenderlo mejor. A lo largo de este recorrido, no solo aprenderás sobre la operación en sí, sino también sobre su importancia y aplicaciones en diferentes contextos. Prepárate para adentrarte en el fascinante mundo de la división, ¡donde cada número cuenta!
1. Definición de la división
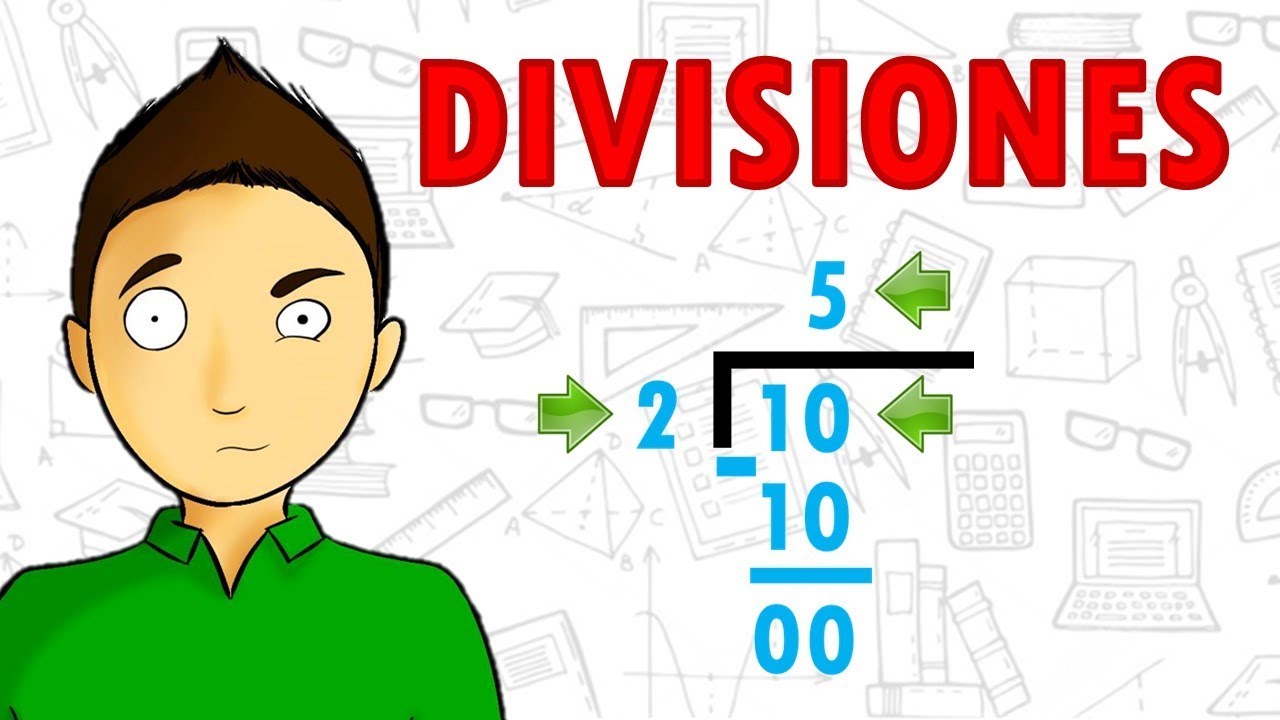
La división es una operación matemática que consiste en repartir una cantidad en partes iguales. En términos simples, se busca determinar cuántas veces un número (llamado dividendo) puede ser dividido por otro número (denominado divisor). El resultado de esta operación se conoce como cociente. Por ejemplo, si tienes 12 manzanas y deseas repartirlas entre 4 amigos, la división te ayuda a saber cuántas manzanas recibe cada uno. En este caso, 12 (dividendo) dividido por 4 (divisor) es igual a 3 (cociente), lo que significa que cada amigo recibe 3 manzanas.
2. Partes de la división
Para entender mejor la división, es fundamental conocer sus partes. Cada división consta de tres elementos principales: el dividendo, el divisor y el cociente. Además, en algunas divisiones, también podemos encontrar un residuo. A continuación, desglosamos cada una de estas partes:
2.1 Dividendo
El dividendo es el número que se va a dividir. En el ejemplo anterior, 12 es el dividendo. Es la cantidad total que se quiere repartir. Comprender el concepto de dividendo es crucial, ya que establece la base de la operación. Si cambiamos el dividendo, el resultado de la división también cambiará. Por ejemplo, si en lugar de 12 manzanas tuviéramos 20, la división sería diferente: 20 dividido por 4 es igual a 5. Esto ilustra cómo el dividendo influye directamente en el resultado.
2.2 Divisor
El divisor es el número por el cual se divide el dividendo. En nuestro ejemplo, el divisor es 4. Este número representa cuántas partes iguales queremos crear. Es importante notar que el divisor no puede ser cero, ya que dividir entre cero no está definido en matemáticas. Por ejemplo, si intentamos dividir 12 entre 0, no obtendremos un resultado válido. El divisor también puede ser un número entero, fraccionario o decimal, lo que agrega más flexibilidad a la operación de división.
2.3 Cociente
El cociente es el resultado de la división. Siguiendo nuestro ejemplo, el cociente de 12 dividido por 4 es 3. El cociente indica cuántas veces el divisor cabe en el dividendo. En situaciones donde el dividendo no se puede dividir exactamente por el divisor, el cociente será un número decimal o fraccionario. Por ejemplo, si dividimos 10 entre 3, el cociente sería 3.33, lo que indica que 3 cabe 3 veces en 10, con un sobrante.
2.4 Residuo
El residuo es la parte que queda después de realizar la división cuando no se puede dividir exactamente. En el caso de 10 dividido por 3, el residuo sería 1, ya que 3 cabe 3 veces en 10 (que es 9), y queda 1. El residuo puede ser útil para entender cómo se distribuyen las cantidades en situaciones prácticas, como al repartir objetos que no se pueden dividir en partes iguales. La presencia del residuo también nos indica que la división no fue exacta y que hay un sobrante que no se pudo repartir.
3. Tipos de división
La división puede clasificarse en varios tipos según su naturaleza y contexto. Entender los diferentes tipos de división puede ser útil en diversas aplicaciones matemáticas. A continuación, exploraremos los más comunes:
3.1 División exacta
Una división se considera exacta cuando el residuo es cero. Esto significa que el dividendo se puede dividir completamente por el divisor. Por ejemplo, 20 dividido por 5 es igual a 4, y no hay residuo. Las divisiones exactas son comunes en situaciones cotidianas, como repartir objetos entre grupos sin que sobre nada.
3.2 División inexacta
En contraste, una división inexacta es aquella en la que el residuo no es cero. Por ejemplo, al dividir 23 entre 5, el cociente es 4 y el residuo es 3. Esto indica que 5 cabe 4 veces en 23, pero hay 3 unidades que no se pueden repartir. Las divisiones inexactas son comunes en situaciones donde no se puede repartir de manera equitativa.
3.3 División entera
La división entera se refiere a la operación que se realiza sin considerar los decimales. Por ejemplo, al dividir 15 entre 4, el cociente es 3 y el residuo es 3, ya que nos centramos únicamente en el número entero. Este tipo de división es útil en situaciones donde solo se necesitan resultados enteros, como al contar objetos.
4. La división en la vida cotidiana
La división no es solo un concepto abstracto; tiene aplicaciones prácticas en nuestra vida diaria. Desde las compras hasta la planificación de eventos, la división nos ayuda a organizar y gestionar recursos de manera efectiva. Aquí hay algunas formas en las que utilizamos la división en situaciones cotidianas:
4.1 Presupuesto y finanzas
Cuando se trata de administrar un presupuesto, la división juega un papel fundamental. Por ejemplo, si tienes un presupuesto mensual de $600 y deseas dividirlo equitativamente entre 4 semanas, simplemente divides 600 entre 4, lo que te da un gasto semanal de $150. Esto te permite planificar tus gastos de manera efectiva y asegurarte de no exceder tu presupuesto.
4.2 Reparto de tareas
En el ámbito laboral o escolar, la división se utiliza para repartir tareas entre un grupo de personas. Si un proyecto debe completarse en 12 horas y hay 3 personas trabajando en él, cada persona debería dedicar aproximadamente 4 horas al proyecto. La división nos ayuda a equilibrar la carga de trabajo y garantizar que todos contribuyan de manera equitativa.
4.3 Cocina y recetas
Cuando se trata de cocinar, la división es esencial para ajustar las porciones de una receta. Si una receta sirve para 6 personas y solo necesitas cocinar para 2, puedes dividir todos los ingredientes por 3. Esto te permite adaptar la receta sin perder la proporción de sabores y cantidades. Así, la división se convierte en una herramienta práctica en la cocina.
5. Ejemplos prácticos de división
Para solidificar nuestra comprensión de la división y sus partes, es útil ver algunos ejemplos prácticos. A continuación, exploramos diferentes situaciones donde la división se aplica:
5.1 Dividiendo objetos
Imagina que tienes 30 galletas y deseas repartirlas entre 6 amigos. Para saber cuántas galletas le toca a cada uno, realizas la división 30 entre 6. El cociente es 5, lo que significa que cada amigo recibirá 5 galletas. Este ejemplo ilustra cómo la división ayuda a repartir objetos de manera equitativa.
5.2 Distribuyendo tiempo
Supongamos que tienes 60 minutos para estudiar para un examen y deseas dividir ese tiempo en 3 sesiones. Para calcular cuánto tiempo dedicarás a cada sesión, divides 60 entre 3, lo que da como resultado 20 minutos por sesión. Esto te permite gestionar tu tiempo de estudio de manera efectiva y asegurarte de cubrir todos los temas necesarios.
5.3 Calculando precios por unidad
Cuando compras productos en el supermercado, a menudo necesitas calcular el precio por unidad para saber cuál es la mejor oferta. Si compras 4 litros de leche por $8, puedes dividir 8 entre 4 para encontrar el precio por litro. En este caso, el precio por litro es $2. Este tipo de cálculo es esencial para tomar decisiones informadas al comprar.
6. Estrategias para enseñar la división
Enseñar la división puede ser un desafío, pero existen diversas estrategias que pueden facilitar el aprendizaje. A continuación, exploramos algunas técnicas efectivas para enseñar este concepto a estudiantes:
6.1 Uso de objetos manipulativos
Los objetos manipulativos, como bloques o fichas, son herramientas efectivas para enseñar la división. Al permitir que los estudiantes visualicen y manipulen los objetos, pueden comprender mejor cómo se reparte una cantidad. Por ejemplo, al dividir 12 bloques entre 3 grupos, los estudiantes pueden contar y ver cómo se distribuyen los bloques, facilitando la comprensión del concepto.
6.2 Juegos y actividades interactivas
Incorporar juegos en el aprendizaje de la división puede hacer que el proceso sea más divertido y atractivo. Juegos como «La carrera de las divisiones» o «Bingo de divisiones» permiten a los estudiantes practicar la división de manera lúdica. Estas actividades no solo refuerzan el concepto, sino que también fomentan la participación y el trabajo en equipo.
6.3 Problemas del mundo real
Presentar problemas de la vida real que involucren la división puede ayudar a los estudiantes a ver la relevancia del concepto. Al plantear situaciones cotidianas, como repartir dinero o calcular el tiempo, los estudiantes pueden aplicar la división en contextos significativos. Esto no solo mejora su comprensión, sino que también les muestra cómo la división es útil en su vida diaria.
Preguntas Frecuentes (FAQ)
¿Qué es la división en matemáticas?
La división es una operación matemática que consiste en repartir un número (dividendo) en partes iguales según otro número (divisor). El resultado de esta operación se llama cociente. Es fundamental para resolver problemas de distribución y compartir cantidades de manera equitativa.
¿Cómo se representa la división?
La división se puede representar de varias maneras, incluyendo el uso de la barra de división (/) o el símbolo de división (÷). Por ejemplo, la división de 10 entre 2 puede escribirse como 10 ÷ 2 o 10/2, y ambos significan lo mismo: cuántas veces 2 cabe en 10.
¿Qué significa un residuo en la división?
El residuo es la cantidad que sobra después de realizar una división cuando el dividendo no se puede dividir exactamente por el divisor. Por ejemplo, al dividir 10 entre 3, el cociente es 3 y el residuo es 1, lo que indica que hay una parte que no se puede repartir equitativamente.
¿Qué es la división larga?
La división larga es un método que se utiliza para dividir números grandes. Implica un proceso paso a paso que desglosa la operación en partes más pequeñas, facilitando la comprensión y el cálculo. Este método es especialmente útil cuando se trabaja con números que no se pueden dividir fácilmente.
¿La división siempre tiene un residuo?
No, la división no siempre tiene un residuo. Cuando el dividendo se puede dividir exactamente por el divisor, el residuo es cero. Por ejemplo, en la división de 8 entre 2, el resultado es 4, y no hay residuo. Sin embargo, en otros casos, como 9 entre 4, habrá un residuo de 1.
¿Cómo se utiliza la división en la vida diaria?
La división se utiliza en numerosas situaciones cotidianas, como repartir dinero, calcular precios por unidad, organizar tareas, y ajustar recetas. Es una herramienta fundamental que nos ayuda a gestionar recursos y tomar decisiones informadas en nuestra vida diaria.
¿Es posible dividir números negativos?
Sí, es posible dividir números negativos. La regla básica es que al dividir dos números con el mismo signo (ambos positivos o ambos negativos), el resultado será positivo. Si los números tienen signos diferentes, el resultado será negativo. Por ejemplo, -10 dividido por 2 es -5, mientras que 10 dividido por -2 también es -5.