Triángulos: Conoce sus Lados y Ángulos de Forma Sencilla y Clara
Los triángulos son figuras geométricas fascinantes que se encuentran en diversas áreas de la vida cotidiana y la ciencia. Desde la arquitectura hasta la naturaleza, estos polígonos de tres lados tienen un papel fundamental en la geometría y más allá. Comprender sus lados y ángulos no solo es crucial para los estudiantes, sino también para cualquier persona interesada en desarrollar habilidades matemáticas prácticas. En este artículo, vamos a explorar el mundo de los triángulos de forma sencilla y clara, desglosando sus características, tipos, propiedades y aplicaciones. Te invito a sumergirte en este viaje que te ayudará a dominar los conceptos básicos de los triángulos, desde sus lados hasta sus ángulos, y todo lo que necesitas saber para utilizarlos en tu vida diaria.
1. ¿Qué es un Triángulo?
Un triángulo es un polígono de tres lados y tres ángulos. La suma de los ángulos internos de cualquier triángulo siempre es igual a 180 grados. Esta propiedad es fundamental y se utiliza en diversas aplicaciones matemáticas y prácticas. Los triángulos pueden clasificarse de varias maneras, lo que los hace aún más interesantes.
1.1 Clasificación de los Triángulos según sus Lados
Los triángulos se pueden clasificar en tres categorías según la longitud de sus lados:
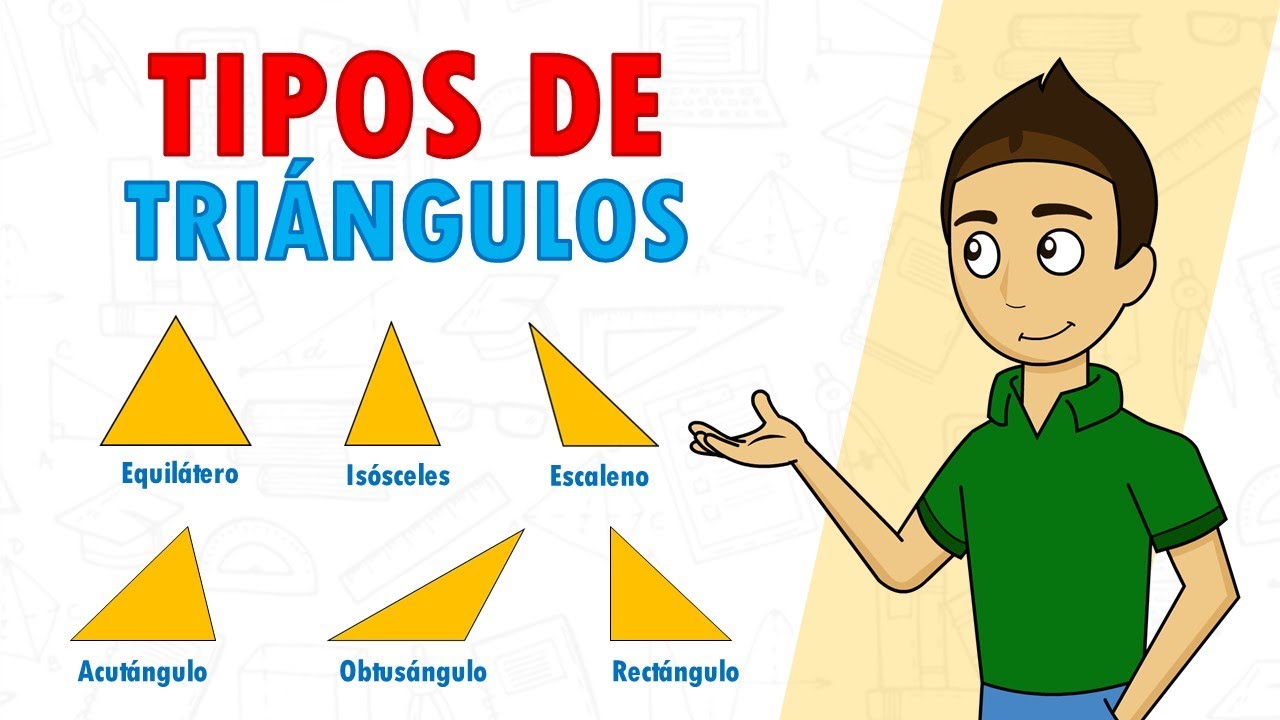
- Triángulo Equilátero: Tiene los tres lados de igual longitud. Cada uno de sus ángulos mide 60 grados.
- Triángulo Isósceles: Posee dos lados de igual longitud. Los ángulos opuestos a estos lados son iguales.
- Triángulo Escaleno: Todos sus lados tienen diferentes longitudes, y, por ende, todos sus ángulos son distintos.
Esta clasificación nos ayuda a entender cómo se comportan los triángulos en diferentes contextos y facilita el estudio de sus propiedades.
1.2 Clasificación de los Triángulos según sus Ángulos
Además de la clasificación por lados, los triángulos también se pueden clasificar según sus ángulos:
- Triángulo Acutángulo: Todos sus ángulos son menores de 90 grados.
- Triángulo Rectángulo: Tiene un ángulo recto, es decir, de 90 grados.
- Triángulo Obtusángulo: Posee un ángulo mayor de 90 grados.
Conocer estas clasificaciones es fundamental para resolver problemas geométricos y entender mejor las propiedades de los triángulos.
2. Propiedades de los Triángulos
Los triángulos tienen propiedades únicas que los distinguen de otras figuras geométricas. Estas propiedades son esenciales para resolver problemas y entender conceptos más avanzados en geometría.
2.1 Suma de Ángulos
Como mencionamos anteriormente, la suma de los ángulos internos de un triángulo siempre es igual a 180 grados. Esta propiedad se aplica a todos los triángulos, independientemente de su tipo. Por ejemplo, si tienes un triángulo con un ángulo de 50 grados y otro de 60 grados, el tercer ángulo se puede calcular restando la suma de estos dos ángulos de 180 grados, lo que resulta en 70 grados.
2.2 Teorema de Pitágoras
En triángulos rectángulos, el Teorema de Pitágoras es una de las herramientas más poderosas. Establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Esta relación se expresa matemáticamente como:
c² = a² + b²
Donde c es la hipotenusa y a y b son los otros dos lados. Esta propiedad es esencial en muchas aplicaciones prácticas, como la construcción y la navegación.
2.3 Desigualdad Triangular
Otra propiedad interesante es la desigualdad triangular, que establece que la suma de las longitudes de dos lados de un triángulo siempre debe ser mayor que la longitud del tercer lado. Por ejemplo, si tienes un triángulo con lados de 3 y 4 unidades, el tercer lado debe ser menor que 7 unidades (3 + 4) y mayor que 1 unidad (4 – 3). Esta propiedad es crucial para determinar si tres longitudes pueden formar un triángulo.
3. Aplicaciones de los Triángulos en la Vida Real
Los triángulos no son solo figuras geométricas abstractas; tienen múltiples aplicaciones prácticas en la vida cotidiana y en diversas disciplinas. Desde la arquitectura hasta la ingeniería, los triángulos son fundamentales.
3.1 Arquitectura y Diseño
En arquitectura, los triángulos se utilizan para crear estructuras estables y resistentes. La forma triangular distribuye el peso de manera uniforme, lo que permite construir edificios altos y puentes seguros. Por ejemplo, las estructuras de truss (arcos) en los puentes utilizan triángulos para maximizar la resistencia y minimizar el material necesario.
En navegación, los triángulos se utilizan en la triangulación para determinar posiciones. Al medir distancias y ángulos desde tres puntos conocidos, se puede calcular la ubicación de un punto desconocido. Esta técnica es fundamental en la cartografía y en la planificación de rutas de viaje.
3.3 Arte y Diseño Gráfico
Los triángulos también tienen un papel importante en el arte y el diseño gráfico. Se utilizan para crear composiciones visuales equilibradas y dinámicas. Los artistas y diseñadores a menudo emplean triángulos para guiar la mirada del espectador y crear una sensación de movimiento o estabilidad.
4. Cómo Calcular el Área de un Triángulo
Calcular el área de un triángulo es una habilidad básica en geometría que tiene múltiples aplicaciones. La fórmula más común para calcular el área es:
Área = (base × altura) / 2
Donde la base es la longitud de uno de los lados y la altura es la distancia perpendicular desde ese lado hasta el vértice opuesto.
4.1 Ejemplo Práctico
Imagina que tienes un triángulo con una base de 10 cm y una altura de 5 cm. Para calcular el área, simplemente multiplicas la base por la altura y divides entre 2:
Área = (10 cm × 5 cm) / 2 = 25 cm²
Esto significa que el área de tu triángulo es de 25 centímetros cuadrados. Este cálculo es fundamental en diversas situaciones, desde la planificación de espacios hasta la agricultura.
4.2 Uso de la Fórmula de Herón
En algunos casos, puede que no tengas la altura de un triángulo, pero sí las longitudes de sus tres lados. En tales situaciones, puedes utilizar la fórmula de Herón para calcular el área:
Área = √[s(s-a)(s-b)(s-c)]
Donde s es el semiperímetro del triángulo, calculado como s = (a + b + c) / 2. Aquí, a, b y c son las longitudes de los lados del triángulo. Esta fórmula es especialmente útil en problemas más complejos donde se requieren cálculos precisos.
5. Triángulos en la Trigonometría
La trigonometría es una rama de la matemática que estudia las relaciones entre los ángulos y los lados de los triángulos, especialmente los triángulos rectángulos. Esta disciplina es esencial en diversas aplicaciones, desde la ingeniería hasta la física.
5.1 Funciones Trigonométricas
Las funciones trigonométricas, como el seno, coseno y tangente, son herramientas fundamentales para trabajar con triángulos. Por ejemplo:
- Seno: Relación entre el cateto opuesto y la hipotenusa.
- Coseno: Relación entre el cateto adyacente y la hipotenusa.
- Tangente: Relación entre el cateto opuesto y el cateto adyacente.
Estas funciones permiten calcular longitudes y ángulos en triángulos rectángulos, lo que es esencial en campos como la navegación y la arquitectura.
5.2 Aplicaciones en la Vida Real
La trigonometría tiene aplicaciones prácticas en la vida diaria. Por ejemplo, los arquitectos utilizan funciones trigonométricas para calcular pendientes y alturas, mientras que los ingenieros pueden calcular fuerzas y tensiones en estructuras. La trigonometría también se aplica en la creación de gráficos y modelos en diseño gráfico.
6. Preguntas Frecuentes (FAQ)
¿Cuántos tipos de triángulos existen?
Existen dos formas principales de clasificar los triángulos: según sus lados y según sus ángulos. Según los lados, tenemos triángulos equiláteros, isósceles y escalenos. Según los ángulos, encontramos triángulos acutángulos, rectángulos y obtusángulos. Cada tipo tiene propiedades únicas que los hacen interesantes y útiles en diferentes contextos.
¿Cómo se mide un triángulo?
Para medir un triángulo, necesitas conocer la longitud de sus lados y sus ángulos. Puedes usar una regla para medir los lados y un transportador para medir los ángulos. Si ya tienes la longitud de los lados, puedes usar la fórmula de Herón para calcular el área, o la fórmula básica de área si conoces la base y la altura.
¿Cuál es la importancia de los triángulos en la geometría?
Los triángulos son fundamentales en geometría porque son las figuras más simples que se pueden formar. A partir de triángulos, se pueden construir otras figuras geométricas más complejas. Además, muchas propiedades geométricas se derivan de las propiedades de los triángulos, lo que los convierte en una base esencial para el estudio de la geometría.
¿Qué es un triángulo rectángulo y por qué es importante?
Un triángulo rectángulo es aquel que tiene un ángulo recto (90 grados). Es importante porque permite aplicar el Teorema de Pitágoras, que relaciona los lados de un triángulo rectángulo. Este tipo de triángulo es fundamental en la construcción, la navegación y muchas otras áreas debido a su simplicidad y propiedades únicas.
¿Cómo se utilizan los triángulos en la arquitectura?
En arquitectura, los triángulos se utilizan para crear estructuras estables y resistentes. La forma triangular distribuye las cargas de manera eficiente, lo que permite construir edificios y puentes que pueden soportar grandes pesos. Los triángulos también se utilizan en el diseño de techos y otras estructuras arquitectónicas para mejorar la estabilidad y la estética.
¿Se pueden encontrar triángulos en la naturaleza?
Sí, los triángulos se encuentran en muchas formas en la naturaleza. Por ejemplo, las estructuras de ciertos cristales, la forma de montañas y la disposición de hojas en algunas plantas pueden exhibir formas triangulares. Además, los triángulos son comunes en la biología, como en la estructura de ciertos organismos y en patrones de crecimiento.
¿Qué herramientas se pueden usar para trabajar con triángulos?
Para trabajar con triángulos, puedes usar varias herramientas, como reglas para medir lados, transportadores para medir ángulos y compases para dibujar triángulos. En entornos más avanzados, también se pueden utilizar software de diseño asistido por computadora (CAD) para crear y manipular triángulos y otras formas geométricas.